Year 8: Combinatorics Dr J Frost ([email protected])
29 Slides1.67 MB

Year 8: Combinatorics Dr J Frost ([email protected]) www.drfrostmaths.com Last modified: 29th December 2015

PART 1 :: Systematic Counting Sometimes the easiest way to count things is to explicitly list out every possibility! The key is listing the possibilities in some systematic way that avoids missing out cases or duplicates. Starter [JMC 2005 Q17] The figure shows rectangle and line , which divides the rectangle into two squares. How many right-angled triangles can be drawn using any three of the points as corners? Hint: Perhaps consider each possible shape of triangle and how many there are of each? 8 ?4 2 14 possibilities. By breaking the problem down into types of triangle, it made it much easier for us to count without missing out any possibilities. It also prevented us having to draw out similar cases.
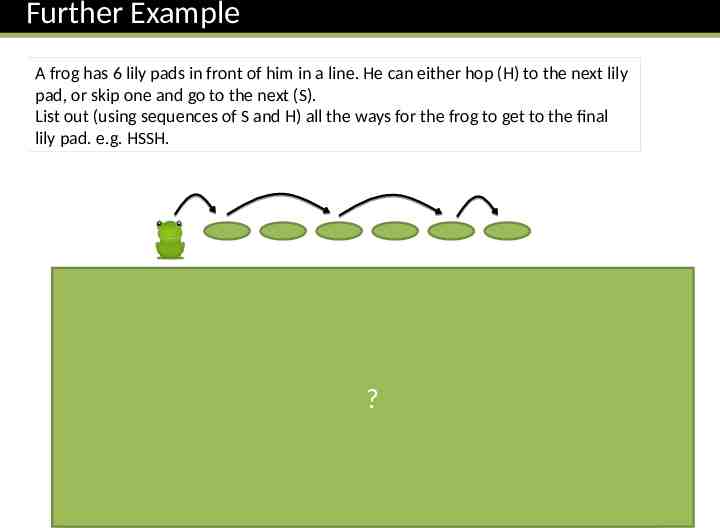
Further Example A frog has 6 lily pads in front of him in a line. He can either hop (H) to the next lily pad, or skip one and go to the next (S). List out (using sequences of S and H) all the ways for the frog to get to the final lily pad. e.g. HSSH. Easiest when we break down into different numbers of skips: 0 skips: HHHHHH (1 way) 1 skip: SHHHH, HSHHH, HHSHH, HHHSH, HHHHS (5 ways) 2 skips: SSHH, SHSH, SHHS, HSSH, HSHS, HHSS (6 ways) To ensure I got all the possibilities here, I gradually moved 3 skips: SSS (1 way) 13 ways. ? the second S right one, before moving the left S right and repeating: SSHH HSSH HHSS SHSH HSHS SHHS In summary, break the problem down into smaller problems where it’s easy to count within each one, e.g. types of triangles, team sizes, number of skips, etc.
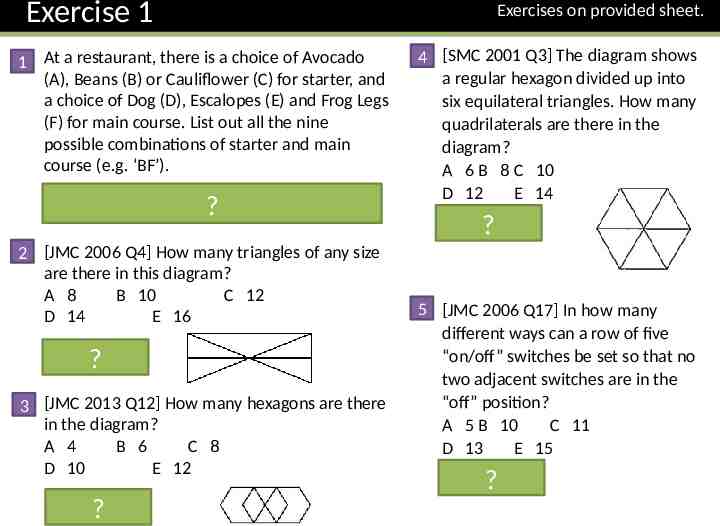
Exercise 1 1 At a restaurant, there is a choice of Avocado (A), Beans (B) or Cauliflower (C) for starter, and a choice of Dog (D), Escalopes (E) and Frog Legs (F) for main course. List out all the nine possible combinations of starter and main course (e.g. ‘BF’). Solution: AD, AE, AF, BD, ? BE, BF, CD, CE, CF. 2 [JMC 2006 Q4] How many triangles of any size are there in this diagram? A 8 B 10 C 12 D 14 E 16 Solution: ? C 3 [JMC 2013 Q12] How many hexagons are there in the diagram? A 4 B 6 C 8 D 10 E 12 Solution: ?E Exercises on provided sheet. 4 [SMC 2001 Q3] The diagram shows a regular hexagon divided up into six equilateral triangles. How many quadrilaterals are there in the diagram? A 6 B 8 C 10 D 12 E 14 Solution: D ? 5 [JMC 2006 Q17] In how many different ways can a row of five “on/off” switches be set so that no two adjacent switches are in the “off” position? A 5 B 10 C 11 D 13 E 15 Solution: D ?
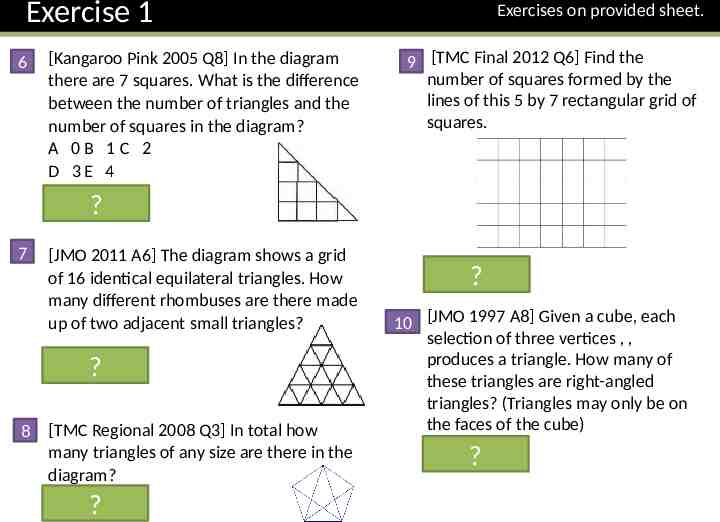
Exercise 1 6 [Kangaroo Pink 2005 Q8] In the diagram there are 7 squares. What is the difference between the number of triangles and the number of squares in the diagram? A 0B 1C 2 D 3E 4 Solution: D Exercises on provided sheet. 9 [TMC Final 2012 Q6] Find the number of squares formed by the lines of this 5 by 7 rectangular grid of squares. ? 7 [JMO 2011 A6] The diagram shows a grid of 16 identical equilateral triangles. How many different rhombuses are there made up of two adjacent small triangles? Solution: ? 18 8 [TMC Regional 2008 Q3] In total how many triangles of any size are there in the diagram? Solution: 35 ? Solution: ? 85 10 [JMO 1997 A8] Given a cube, each selection of three vertices , , produces a triangle. How many of these triangles are right-angled triangles? (Triangles may only be on the faces of the cube) Solution: 24 ?

Exercise 1 11 Each hour a pirate ship can either sail 1km West (W), 1km East (E), 1km North (N) or 1km South (S). It must always be moving. List all the ways in which the ship can end up 2km North after 4 hours (e.g. ‘NNWE’) and count the number of possible journeys. (Hint: it may help to break the problem down possible sets of four movements, e.g. a N, N, W and E, and then considering the possible orderings of each possible set). Solution: NNWE, NNEW, NWNE, NENW, NWEN, NEWN, WNNE, ENNW, ? EWNN, WNEN, ENWN, WENN, SNNN, NSNN, NNSN, NNNS (16 ways). Exercises on provided sheet. 12 [TMC Regional 2014 Q4] Every day Keith has a breakfast, a lunch and a dinner. The options for each meal are: One day Keith eats four items. In how many different ways can he do this? Solution: 12 ? 13 [JMO 2004 A10] The Famous Five have been given 20 sweets as a reward for solving a tricky crime. They have agreed that the oldest of them must receive more than the next oldest, who must receive more than the next oldest, and so on. Assuming that each of the five gets at least one sweet, in how many different ways can they share the sweets? Solution: ? 7
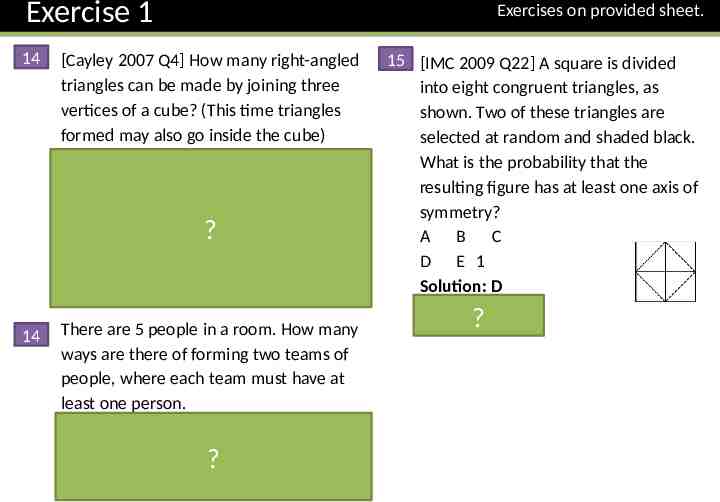
Exercise 1 14 [Cayley 2007 Q4] How many right-angled triangles can be made by joining three vertices of a cube? (This time triangles formed may also go inside the cube) Solution: 48 (In a previous question we found 24 triangles on the faces. A further 24 triangles can be formed, 2 for each face diagonal where?the triangle will pass inside the cube, e.g:). 14 There are 5 people in a room. How many ways are there of forming two teams of people, where each team must have at least one person. Solution: 15 teams. (5 teams where the teams are split 1 and?5. 10 teams where the teams are split 2 and 3) Exercises on provided sheet. 15 [IMC 2009 Q22] A square is divided into eight congruent triangles, as shown. Two of these triangles are selected at random and shaded black. What is the probability that the resulting figure has at least one axis of symmetry? A B C D E 1 Solution: D ?

PART 2 :: Counting by Multiplying Starter: Suppose the alphabet was limited to just A, B, C, D. Fold your provided piece of paper into 16 parts. Put ‘A’ 4 times, ‘B’ 4 times, ‘C’ 4 times and ‘D’ 4 times, before cutting. Use these cards (or otherwise) to answer the following questions: Note: a ‘word’ is any possible sequence of characters; it need not be in a dictionary. Question 1 Question 2 Question 3 The number of possible 2 letter ‘words’ where the letters are different. The number of possible 2 letter ‘words’ where the letters are unrestricted. 4 possibilities for first letter, 3 for ? the second. 4 possibilities for first letter, 4 for the ? second. The number of possible 3 letter ‘words’ where each letter cannot be the same as the previous letter, but is otherwise unrestricted. Question 4 Question N Question NN The number of 4 letters words using each of the letters A, B, C, D exactly once. The number of 5 letter words using the letters AABCD, each exactly once. The number of 10 letter words using the letters AAAAAABBCD each once. 𝟓 𝟒 𝟑 𝟐 𝟔𝟎 ? 𝟐 𝟏𝟎 ! 𝟐𝟓𝟐𝟎 𝟔!𝟐! ? 𝟒 𝟑 𝟐? 𝟏 𝟐𝟒 𝟒 𝟑 𝟑 𝟑𝟔 ?

Multiplying and Factorial Function If the number of choices for each ‘thing’ are independent of each other, then we can multiply them together to get the total number of combinations. ABCDEFGHIJKLMNOPQRSTUVWXYZ For a full alphabet of 26 letters: a) How many possible 3 letter ‘words’ are there? There are 26 choices for each letter. ? b) How many possible 3 letter ‘words’ are there, where all letters are different? Each time there is one less choice. ? c) How many possible ways are there of arranging the letters of the word MATHS? There are 5 choices for the first letter, then 4 for the next, and so on. ? ! is said “5 factorial”. means the number of ways of arranging distinct objects in a line.

Examples Q I throw 4 dice. How many possible outcomes are there? ? Q I throw 10 coins. How many possible outcomes are there? ? Q I have a 10 kittens. I pick up 4 kittens and put them in a line. How many possibilities are there? Note that the ordering of kittens in the line matters in ? this scenario (the number of possibilities would be less if we only cared about what kittens were selected)

A Few More Examples Q I have 6 different coloured balls in a line. How many ways of arranging them? ? Q 3 boys and 4 girls go to a cinema. How many ways of arranging them such that the boys all come before the girls? ? Q How many ways of arranging the letters in the word BANANA? If the letters were all different there would be ways. However, for example would count as the same as because the N’s aren’t distinguishable. So we need to divide by 2 to avoid duplicates. Similarly there are ways the A’s could have been arranged ? which would lead to the same possibility. Thus:
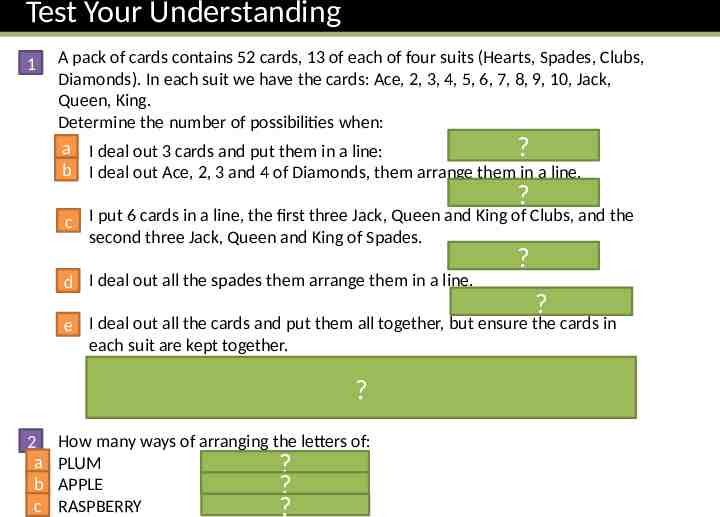
Test Your Understanding 1 A pack of cards contains 52 cards, 13 of each of four suits (Hearts, Spades, Clubs, Diamonds). In each suit we have the cards: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King. Determine the number of possibilities when: a I deal out 3 cards and put them in a line: ? b I deal out Ace, 2, 3 and 4 of Diamonds, them arrange them in a line. ? c I put 6 cards in a line, the first three Jack, Queen and King of Clubs, and the second three Jack, Queen and King of Spades. d I deal out all the spades them arrange them in a line. ? ? e I deal out all the cards and put them all together, but ensure the cards in each suit are kept together. There are ways or arranging the clubs, ways of arranging the spades, etc. But there’s also 4! ways of arranging?the four blocks of cards. 2 a b c How many ways of arranging the letters of: PLUM ? APPLE ? RASPBERRY ?

Exercise 2 Exercises on provided sheet. 1 A queue in the post office consists of a cat, a dog and a llama. How many possible orderings are there of animals in the line? Solution: ? 2 A bag contains 8 different coloured balls. I pick 4 of them and put them in a line. How many ways are there of doing this? Solution: ? 4 How many ways are there of arranging the letters in the words: a. SMURF b. BOTTLE c. CABBAGE d. TITILLATION ? ? ? ? 5 [TMC Regional 2009 Q1] A tile is fixed to a wall and then painted with four different colours, one for each quarter. One way of doing this is 3 I have cards with the number 1, 2, 3, 4 on them. I have a plentiful supply of each. How many ways are there of: a. Putting four numbers in a line where all numbers must be different. b. Putting four numbers in a line where we are unrestricted in choices of numbers. c. Putting four numbers in a line where each number must not be the same as the one immediately before. d. Forming a four digit number starting with 3. ? ? ? ? In how many other ways may the tile be painted? ? 6 [JMO 1999 A5] UKMT, TMUK and KTUM are all different arrangements of the letters U, K, M and T. If the number of all the different arrangements of these four letters is and the number of all the different arrangements of the letters and is , what is the value of ? Solution: ?

Exercise 2 7 Exercises on provided sheet. [JMC 2013 Q25] For Beatrix’s latest art installation, she has fixed a square sheet of steel to a wall. She has two magnetic tiles, both which she attaches to the steel sheet, in any orientation, so that none of the sheet is visible and the line separating the two tiles cannot be seen. As shown alongside, one tile has one black cell and one grey cell; the other tile has one black cell and one spotted cell. How many different looking installations can Beatrix obtain? A 4 B 8 C 12 D 14 E 24 Solution: C The dotted tile can go in 4 positions. This leaves 3 positions for the grey tile. The rest are filled with black (with no choice involved). ? 8 [TMC Regional 2013 Q8] Claire, David, Jean and Richard are queuing for the bus. In how many different ways can they line up in single file, one behind the other, without Jean being last? ? Solution: Starting from the back [Kangaroo Pink 2015 Q18] Petra has 9 three different dictionaries and two different novels on a shelf. How many ways are there to arrange the books if she wants to keep the dictionaries together and the novels together? A 12 B 24C 30 D 60 E 120 Solution: B (Can either have booksnovels or novels-book, giving 2 lots of ) ?

Exercise 2 10 [IMC 2015 Q20] A voucher code is made up of four characters. The first is a letter: V, X or P. The second and third are different digits. The fourth is the units digit of the sum of the second and third digits. How many different voucher codes like this are there? A 180 B 243 C 270 D 300 E 2700 Solution: C. 3 choices for first character. 10 choices for second character and 9 for third (since a different digit). There is no element of choice for the fourth ? character as it is determined by the second and third. Exercises on provided sheet. 11 [IMC 2008 Q23] Beatrix has a 24-hour digital clock on a glass table-top next to her desk. When she looked at the clock at 13:08, she noticed that the reflected display also read 13:08, as shown. How many times in a 24-hour period do the display and its reflection give the same time? A 12 B 36 C 48 D 72 E 96 Solution: E. First note that 0, 1, 3 and 8 reflect. ?

Exercise 2 12 Exercises on provided sheet. [Kangaroo Grey 2006 Q16/Pink 2006 Q19] A train consists of five carriages: I, II, III, IV and V. In how many ways can the carriages be arranged so that carriage I is nearer to the locomotive than carriage II is? A 120 B 60 C 48 D 30 E 10 Solution: B Long way: I is in 1st position: ways of arranging remaining carriages. I is in 2nd position: ways I is in 3rd position: ways ? I is in 4th position: ways ways Really Short way: In half of the ways of arranging the five carriages, I will appear before II.

The ‘Choose’ Function 𝐵1 𝐵2 𝐵3 𝐵4 𝐵 5 How many ways are there of selecting 2 balls from the 5? (such that the order of the balls in my selection does not matter) There are 5 balls for our first choice. There are then 4 balls to choose from. This initially gives 20 possibilities. ? However, for example would represent the same choice as . We therefore have to divide by 2 to avoid duplicates. There are 10 possible selections. (often written ), said “ choose ”, is the number of ways of ‘choosing’ items from without duplicates, such that order does not matter.

Practise using the formula (and your calculator) 9! 9 84 ? 3 3!6! ( ) 10 ! 10 ? 10 1 1!9! ( ) Broculator Tip: Use the button on your calculator (SHIFT ) to calculate directly. 4! 4 ? 1 0 0 ! 1! ( ) What would we expect this to be? (The number of ways of choosing 0 items from 4) What would we expect this to be? (The number of ways of choosing 1 item from 10) Note that ‘no selection’ is itself a choice! Bro Side Note: The choose formula only works if
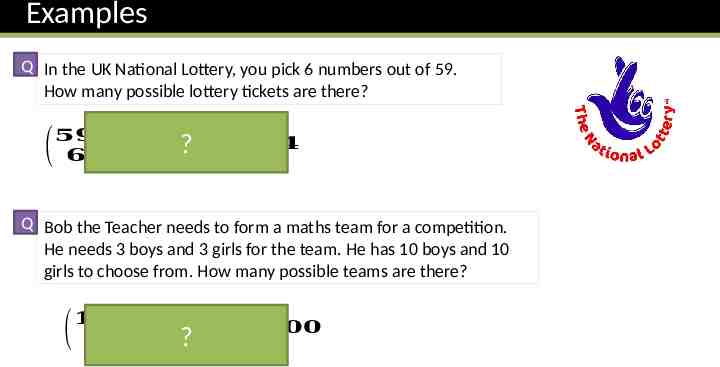
Examples Q In the UK National Lottery, you pick 6 numbers out of 59. How many possible lottery tickets are there? ( 𝟓𝟗 𝟒𝟓 𝟎𝟓𝟕 𝟒𝟕𝟒 𝟔 ) ? Q Bob the Teacher needs to form a maths team for a competition. He needs 3 boys and 3 girls for the team. He has 10 boys and 10 girls to choose from. How many possible teams are there? ( 𝟏𝟎 𝟏𝟎 𝟏𝟒 𝟒𝟎𝟎 𝟑 𝟑 ) ( ?)
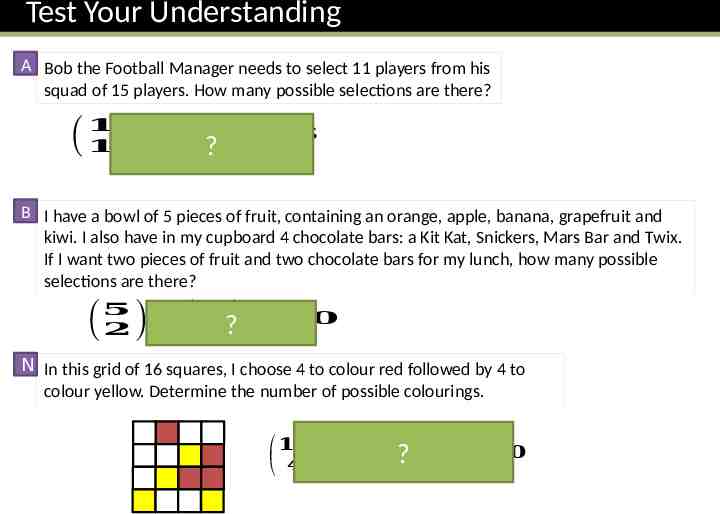
Test Your Understanding A Bob the Football Manager needs to select 11 players from his squad of 15 players. How many possible selections are there? ( 𝟏𝟓 𝟏𝟏 ) 𝟏𝟑𝟔𝟓 ? B I have a bowl of 5 pieces of fruit, containing an orange, apple, banana, grapefruit and kiwi. I also have in my cupboard 4 chocolate bars: a Kit Kat, Snickers, Mars Bar and Twix. If I want two pieces of fruit and two chocolate bars for my lunch, how many possible selections are there? 𝟓 𝟐 𝟒 𝟐 ( ) ( ?) 𝟔𝟎 N In this grid of 16 squares, I choose 4 to colour red followed by 4 to colour yellow. Determine the number of possible colourings. 𝟏𝟔 𝟏 𝟐 𝟗𝟎𝟎𝟗𝟎𝟎 𝟒 𝟒 ( ) ( )?
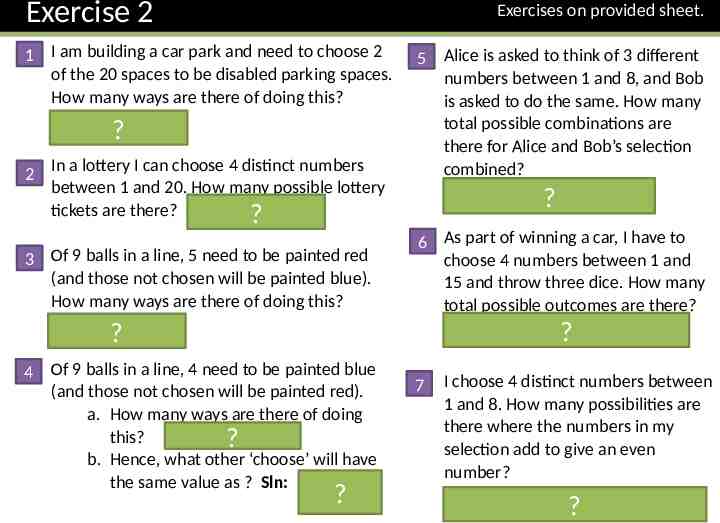
Exercise 2 Exercises on provided sheet. 1 I am building a car park and need to choose 2 of the 20 spaces to be disabled parking spaces. How many ways are there of doing this? Solution: 190 ? 2 In a lottery I can choose 4 distinct numbers between 1 and 20. How many possible lottery tickets are there? Solution:?4845 3 Of 9 balls in a line, 5 need to be painted red (and those not chosen will be painted blue). How many ways are there of doing this? Solution: 126 ? 4 Of 9 balls in a line, 4 need to be painted blue (and those not chosen will be painted red). a. How many ways are there of doing this? Solution: ? 126 b. Hence, what other ‘choose’ will have the same value as ? Sln: ? 5 Alice is asked to think of 3 different numbers between 1 and 8, and Bob is asked to do the same. How many total possible combinations are there for Alice and Bob’s selection combined? Solution: ? 6 As part of winning a car, I have to choose 4 numbers between 1 and 15 and throw three dice. How many total possible outcomes are there? Solution: ? 7 I choose 4 distinct numbers between 1 and 8. How many possibilities are there where the numbers in my selection add to give an even number? Solution: It will be ? half of them. 35

Exercise 2 8 Exercises on provided sheet. Use your calculator to write on a row in your book. On the next row write and . On the next row write and . Continue this pattern for a few more rows, where the top number increases by 1 for each row, and the bottom number varies between 0 and the top number. a. What do you notice about the numbers you get in your structure? You get Pascal’s Triangle! b. Add up the numbers in each row (your first two totals should be 1 and ? 2). What do you notice? You get powers of 2! 9 A beaver travels from the bottom-left hand corner to the top-right corner of a grid, each time only making up or right movements. One possible paths is as pictured. a. How many possible paths are there? Solution: Of the 8 moves 4 need to be right moves. ? (Hint: write a few possible paths as a sequence of arrows, e.g. . What’s always the same about such valid sequences of moves?) b. If the beaver is travelling across a grid, write an expression for the total number of paths in terms of . Solution: ? ? Start Finish

Exercise 2 N Exercises on provided sheet. I choose 5 numbers between 1 and 20. How many choices are there such that the range of the numbers in my selection is 6? Solution: Suppose the smallest number was 1 and the largest 7. Then the remaining three numbers can be chosen between 2 and 6, giving possibilities. We’ll have the same number of ? possibilities where the smallest and largest numbers are 2 and 8, and so on, up to 14 and 20. That’s possibilities.
Levelled Activity Level 3 Level 2 Level 1 (Teacher Note: See printout) Instructions: You may work in pairs. Start on the Level 1 problems provided, recording your answer on this sheet. Answers to Level 1 questions are at the front of the class. Once you’ve checked your answers, go to your teacher and ask for Level 2. You will need to ask the teacher to check your answers to Level 2 and beyond. Solutions are on the next slides.

Level 1 Solutions 1 How many possible 3 letters ‘words’ are there using letters from the English alphabet. Solution: ? 5 How many ways can I arrange 6 books on a shelf? Solution: ? 2 I take 4 items from 7 and put them in a line. How many possibilities are there? Solution: ? 6 How many ways can you arrange the letters of the word CATTLE? Solution: ? 3 From 9 people I choose 4 people to form a team. How many possible teams are there? Solution: ? How many squares of any size are in this 4 diagram? Solution: ? 7 [JMC 2000 Q11] The digits of this year, 2000 A.D., add up to 2. In how many other years since 1 A.D. has this happened? Solution: 9 ? [JMC 2007 Q7] The equilateral 8 triangle is fixed in position. Two of the four small triangles are to be painted black and the other two are to be painted white. In how many different ways can this be done? Solution: ?

Level 2 Solutions 1 How many possible combinations of outcomes are there from the throw of three dice and five coins? Solution: ? 2 [JMO 2006 A4] An equilateral triangle is drawn on a sheet of white card and divided into three identical regions as shown. Then each region is painted red or yellow or blue. More than one region may be painted in the same colour. How many different painted triangles can be made in this way? (Rotating a triangle does not make it different.) Solution: 11 ? 3 [JMO 2008 A4] How many three-digit numbers have the product of their digits equal to 6? Solution: 9? 4 [TMC Regional 2012 Q9] In how many ways can you split your team of 4 people into two separate teams, so that there is at least one person in each team? Solution: 7?ways 5 [Kangaroo Grey 2009 Q16] How many ten-digit numbers are there which contain only the digits 1, 2 or 3, and in which any pair of adjacent digits differs by 1? A 16 B 32 C 64 D 80 E 100 Solution: C. If the number starts with 2, the next is 1 or 3, the next is 2, and so on. When we don’t have a 2 we have two choices, so . But we could had 2 second, giving another 32 possibilities. ?

Level 3 Solutions 1 [Cayley 2008 Q1] How many four-digit multiples of 9 consist of four different odd digits? Solution: 24. Digits have to add up to multiple of 9: only possibility for digits is 1359. There’s 4! ways of arranging these. ? 2 [IMC 2010 Q24] A new taxi firm needs a memorable phone number. They want a number which has a maximum of two different digits. Their phone number must start with the digit 3 and be six digits long. How many such numbers are possible? A 288 B 280 C 279 D 226 E 225 If other digit is different 0, then there are 2 choices for each of the 5 other digits, giving possibilities. However, we want to exclude the case where they’re all 3s (for the moment), giving 31 possibilities There’s 9 numbers this other digit could be giving . Then we count the one possibility where all the digits are 3, giving 280. ? 3 [SMC 2005 Q16] A hockey team consists of 1 goalkeeper, 4 defenders, 4 midfielders and 2 forwards. There are 4 substitutes: 1 goalkeeper, 1 defender, 1 midfielders and 1 forward. A substitute may only replace a player of the same category, e.g. midfielder for midfielders. Given that a maximum of 3 substitutes may be used and that there are still 11 players on the pitch at the end, how many different teams could finish the game? A 110 B 118 C 121 D 125 E 132 Solution: ? B
Level 3 Solutions 6 [Kangaroo Pink 2007 Q24] At a party, five 4 [JMO 2004 A10] The Famous Five have been girls give each other gifts in such a way given 20 sweets as a reward for solving a tricky that everybody gives one gift and crime. They have agreed that the oldest of everybody receives one (though of course them must receive more than the next oldest, nobody receives their own gift). How who must receive more than the next oldest, many possible ways are there for this to and so on. Assuming that each of the five gets happen? at least one sweet, in how many different ways A 5 B 10C 44 can they share the sweets? D 50 E 120 Solution: 7 Solution: C. Suppose the girls are ABCDE. ? 5 [JMO 2002 B1] A number like 4679 is called an ascending number because each digit in the number is larger than the preceding one. (i) How many ascending numbers are there between 1000 and 2000? (ii) How many ascending numbers are there between 1000 and 10000? Solution: 56?and 126 Then to avoid giving themselves a present, we either have to have a ‘cycle’ of 3 and 2 (e.g. ABC give each other presents, and DE give each other one) or a ‘cycle’ of 5. There are possible groupings for 2-3 cycles, where for each there’s only 2 possible giving of presents, giving 20 possibilities. If the cycle is 5, then there’s possibilities (as A had 4 people he can give his present to, then B has 3, etc.) ?

Level 3 Solutions 7 [SMC 2001 Q21] A postman’s sack contains five letters, one each for the five houses in Cayley Close. Mischievously, he posts one letter through each door without looking to see if it is the correct address. In how many different ways could he do this so that exactly two of the five houses receive the correct letters? A 5 B 10 C 20 D 30 E 60 There are ways in which we could choose 2 houses to receive the correct letter. Then of the remaining 3 houses, there are only 2 ways in which they could receive the wrong letter (if the houses are ABC, then the letters could be BCA or CAB). That gives ways. ?






