Topic Topic 8: 8: Optimisation Optimisation of of functions functions
24 Slides370.50 KB

Topic Topic 8: 8: Optimisation Optimisation of of functions functions of of several several variables variables Unconstrained Optimisation (Maximisation and Minimisation) Jacques (4th Edition): 5.4 1
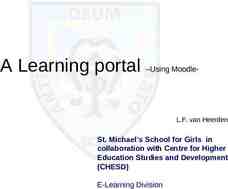
Recall Y Max Min X 2
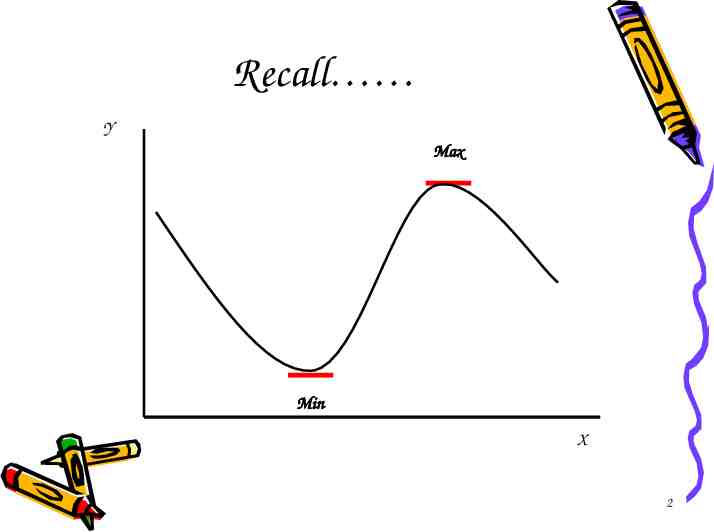
Max Y f (X) X* First-Order / Necessary Condition: dY/dX f (X) 0 Second-Order / Sufficent Condition: d2Y/dX2 f (X) if 0 (Min) if 0 (Max) 3

Re-writing in terms of total differentials . Max Y f (X) X* Necessary Condition: dY f (X).dX 0 , so it must be that f (X) 0 Sufficent Condition: d2Y f (X).dX2 0 for Min 0 for Max For Positive Definite, (Min ), it must be that f 0 Negative Definite, (Max), it must be that f 0 4
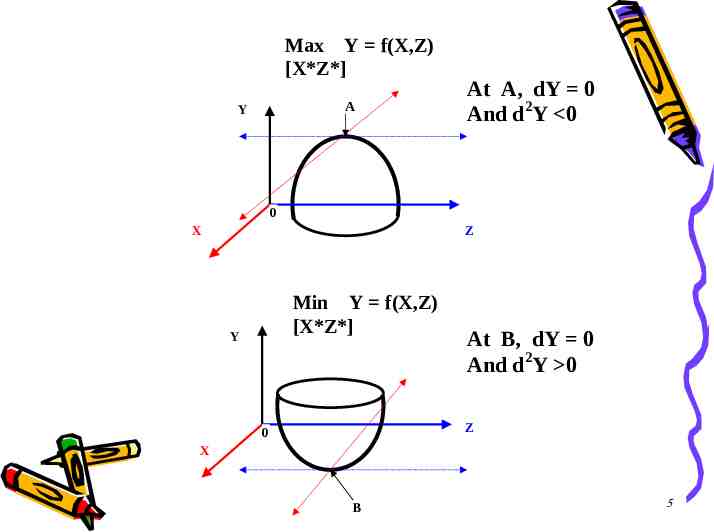
Max Y f(X,Z) [X*Z*] A Y At A, dY 0 And d2Y 0 0 X Z Min Y f(X,Z) [X*Z*] Y At B, dY 0 And d2Y 0 Z 0 X B 5

Max Y f (X, Z) [X*, Z*] Necessary Condition: dY fX.dX fZ.dZ 0 so it must be that fX 0 AND fZ 0 Sufficient Condition: d2Y fXX.dX2 fZX dZ.dX fZZ.dZ2 fXZ .dXdZ .and since fZX fXZ d2Y fXX.dX2 fZZ.dZ2 2fXZ dX.dZ ? 0 for Min 0 for Max Sign Positive Definite Min Sign Negative Definite Max 6

d2Y fXX.dX2 fZZ.dZ2 2fXZ dX.dZ Complete the Square 2 d Y f XX f XZ dX dZ f XX 2 2 f f ZZ f XZ 2 XX dZ f XX Sign Positive Definite To ensure d2Y 0 and Min: f XX 0 and f XX f ZZ f XZ f ZX 0 Sign Negative Definite To ensure d2Y 0 and Max: f XX 0 and note: fXZ.fZX (fXZ)2 f XX f ZZ f XZ f ZX 0 7

Optimisation - A summing Up Condition Neccesary Y f(X) dY 0 Y f(X,Z) dY 0 So required that . fX 0 fX 0 AND fZ 0 Sufficient For Min d2Y 0 d2Y 0 So required that . fXX 0 fXX 0 AND fXX fZZ – (fXZ)2 0 Sufficient For Max d2Y 0 d2Y 0 So required that . fXX 0 fXX 0 AND fXX fZZ – (fXZ)2 0 fXX fZZ – (fXZ)2 0 Saddle Point 8

Examples Find all the maximum and minimum values of the functions: (i) y 10 20 x 2 x 2 16 z z 2 2 xz Necessary Condition for max or min: 1. f x 20 4 x 2 z 0 and 2. f z 16 2 z 2 x 0 Solve simultaneously 2 z 4 x 20 2 z 2 x 16 So 4 x 20 2 x 16 x 2 Subbing in x 2 to eq. 1 (or 2): 2 z 12 and z 6 There is 1 stationary point at (2,6) 9

S e c o n d O rd e r C o n d itio n s : f xx 4 0 f zz 2 0 f xz 2 T hus, 2 fX X fZZ – (fX Z) (-4 .-2 ) – ( -2 ) 2 8 – 4 4 0 S u ffic ie n t c o n d itio n fo r M a x (d 2Y 0 ). fxx 0 a n d fX X fZZ – (fX Z)2 0 S o , M a x a t ( 2 ,6 ) 10

Example 2 ( i i ) y 100 5 x 4 x 2 9 z 5 z 2 8 xz N e c e s s a ry C o n d itio n fo r m a x o r m in : 1. fx 5 8 x 8 z 0 and 2 . f z 9 10 z 8 x 0 S o lv e s im u lta n e o u s ly 8x 5 8z 8 x 9 10 z 5 8 z 9 10 z 2 z 4 z 2 S u b b in g in z 2 to e q 1 (o r 2 ) 8 x 5 8 2 11 x 11 8 T h e r e i s 1 s t a t i o n a r y p o i n t a t 11 8 , 2 11

Second Order Conditions f xx 8 0 f zz 10 0 f xz 8 fXX fZZ – (fXZ)2 (8.10) – (82) 80 – 64 16 . 0 2 Sufficient condition for Min(d Y 0). 2 fxx 0 and fXX fZZ – (fXZ) 0 So, Min at 11 8 ,2 12

Example 3 x2 y 20 x 2 z 2 5z 2 (iii) Necessary Condition for max or min: 1. f x 20 x 0 and 2. f z 4 z 5 0 z 5 4 Thus, x 20 and There is 1 stationary point at 20, 5 4 Second Order Conditions f xx 1 0 f zz 4 0 f xz 0 fXX fZZ – (fXZ)2 (-1.4) – (02) - 4 0 Since, fxx 0 and fXX fZZ – (fXZ)2 0, Saddle Point at 20, 5 4 13

Optimisation Optimisation of of functions functions of of several several variables variables Economic Applications 14

Example 1 A firm can sell its product in two countries, A and B, where demand in country A is given by PA 100 – 2QA and in country B is PB 100 – QB. It’s total output is QA QB, which it can produce at a cost of TC 50(QA QB) ½ (QA QB)2 How much will it sell in the two countries assuming it maximises profits? 15

Objective Function to Max is Profit . TR - TC PAQA PBQB – TC PAQA (100 – 2QA)QA PBQB (100 – QB) QB 100QA – 2QA2 100QB – QB2 – 50QA – 50QB – ½ (QA QB)2 50QA – 2QA2 50QB – QB2 – ½ (QA QB)2 Select QA and QB to max : 16

if 50QA – 2QA2 50QB – QB2 – ½ (QA QB)2 F.O.C. d 0 QA 50 - 4QA – ½ *2 (QA QB) 0 50 - 5QA – QB 0 QB (1) 50 - 2QB – ½ *2 (QA QB) 0 50 - 3QB – QA 0 (2) 50 - 5QA – QB 50 - 3QB – QA 2QA QB Thus, output at stationary point is 2/ ) 7 (QA,QB) (71/7, 14 17

Check Sufficient conditions for Max: d2 0 QA 50 - 5QA – QB QB 50 - 3QB – QA Then QAQA – 5 0 QAQA. QBQB – ( QAQB)2 0 (–5 * –3)) – (-1) 2 14 0 Max So firm max profits by selling 71/7 units to country A and 14 2/7 units to country B. 18

Example 2 Profits and production Max PQ(L, K) – wL - rK {L*, K*} Total Revenue PQ Expenditure on labour L wL Expenditure on Capital K rK Find the values of L & K that max 19

Necessary Condition: d 0 L PQL – w 0 , MPL QL w/P K PQK – r 0 , MPK QK r/P Sufficient Condition for a max, d2 0 So LL 0 AND ( LL. KK - LK. KL) 0 20

NOW, let Q K1/3L1/2, P 2, w 1, r 1/3 Find the values of L & K that max ? Max 2 K1/3L1/2 – L – 1/3 K {L*, K*} Necessary condition for Max: d 0 (1) L K1/3L-1/2 – 1 0 (2) K 2/3 K-2/3 L1/2 – 1/3 0 Stationary point at [L*, K*] [4, 8] note: to solve, from eq1: L½ K1/3 . Substituting into eq2 then, /3K– 2/3K1/3 1/3. Re-arranging K– 1/3 ½ and so K 1/3 2 L½. 2 Thus, K* 23 8. And so L* 22 4. 21

For sufficient condition for a max, Check d2 0; LL 0 & ( LL. KK - LK. KL) 0 L K1/3L-1/2 – 1 K 2/3 K-2/3 L1/2 – 1/3 LL -1/2K1/3L-3/2 0 for all K and L KK – 4/9 K–5/3L½ KL LK 1/3K–2/3L-½ 22
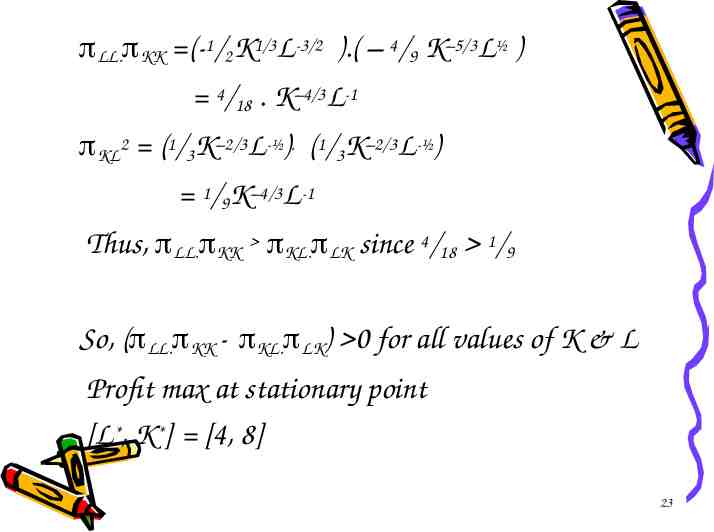
LL. KK (-1/2K1/3L-3/2 ).( – 4/9 K–5/3L½ ) 4/18 . K–4/3L-1 KL2 (1/3K–2/3L-½). (1/3K–2/3L-½) 1/9K–4/3L-1 Thus, LL. KK KL. LK since 4/18 1/9 So, ( LL. KK - KL. LK) 0 for all values of K & L Profit max at stationary point [L*, K*] [4, 8] 23

Unconstrained Optimisation – Functions of Several Variables Self-Assessment Questions on Website Tutorial problem sheets Pass Exam Papers Examples in the Textbook 24