Sequences & Summations CS 1050 Rosen 3.2
14 Slides83.50 KB

Sequences & Summations CS 1050 Rosen 3.2

Sequence A sequence is a discrete structure used to represent an ordered list. A sequence is a function from a subset of the set of integers (usually either the set {0,1,2,. . .} or {1,2, 3,. . .}to a set S. We use the notation an to denote the image of the integer n. We call an a term of the sequence. Notation to represent sequence is {an}

Examples {1, 1/2, 1/3, 1/4, . . .} or the sequence {an} where an 1/n, n Z . {1,2,4,8,16, . . .} {an} where an 2n, n N. {12,22,32,42,. . .} {an} where an n2, n Z

Common Sequences Arithmetic a, a d, a 2d, a 3d, a 4d, n2 1, 4, 9, 16, 25, . . . n3 1, 8, 27, 64, 125, . . . n4 1, 16, 81, 256, 625, . . . 2n 2, 4, 8, 16, 32, . . . 3n 3, 9, 27, 81, 243, . . . n! 1, 2, 6, 24, 120, . . .

Summations Notation for describing the sum of the terms am 1, . . ., an from the sequence, {an} am, n am am 1 . . . an aj j m j is the index of summation (dummy variable) The index of summation runs through all integers from its lower limit, m, to its upper limit, n.
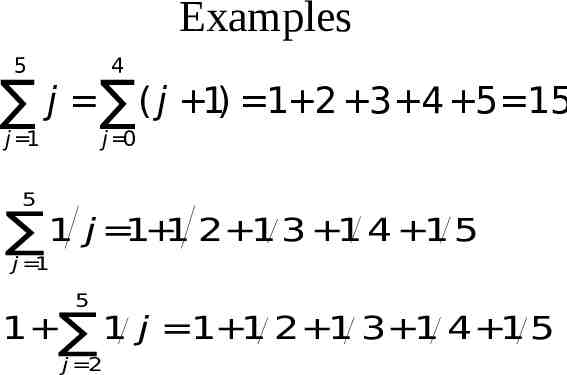
Examples 5 4 j 1 j 0 j ( j 1) 1 2 3 4 5 15 5 1 j 1 1 2 1 3 1 4 1 5 j 1 5 1 1 j 1 1 2 1 3 1 4 1 5 j 2

Summations follow all the rules of multiplication and addition! n n j 1 j 1 c j cj c(1 2 n) c 2c nc n n r ar ar j j 0 n 1 ar j 1 j 0 n n 1 ar k 1 ar ar k 1 k k n 1 n a ar k 0 k

Telescoping Sums n (a a j ) (a1 a0 ) (a2 a1) j 1 j 1 (a3 a2 ) . (an an 1) an a0 Example 4 2 2 [k (k 1) ] k 1 2 2 2 2 2 2 2 2 (1 0 ) (2 1 ) (3 2 ) (4 3 ) 2 4 16 0 16

Closed Form Solutions A simple formula that can be used to calculate a sum without doing all the additions. Example: n n(n 1) k 2 k 1 Proof: First we note that k2 - (k-1)2 k2 - (k2-2k 1) 2k-1. Since k2-(k-1)2 2k-1, then we can sum each side from k 1 to k n n n [k 2 k 1 (k 1) ] (2k 1) 2 k 1

Proof (cont.) n [k 2 k 1 n [k 2 k 1 n (k 1) ] (2k 1) 2 k 1 n n k 1 k 1 (k 1) ] 2k ( 1) 2 n n 0 2 (k) n 2 2 k 1 n n n 2 (k) 2 k 1 n n2 n k 2 k 1

Closed Form Solutions to Sums n j 0 1 . n n(n 1)/ 2 j 0 n j 2 2 2 2 0 1 . n n(n 1)(2n 1)/6 j 0 n 2 2 n (n 1) k 4 k 1 n 3 n 1 ar a k ar ,r 1 r 1 k 0
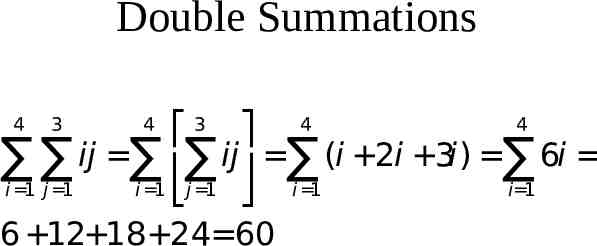
Double Summations 4 3 4 ij ij (i 2i 3i ) 6i i 1 j 1 i 1 j 1 i 1 i 1 4 3 4 6 12 18 24 60

Cardinality Earlier we defined cardinality of a set as the number of elements in the set. We can extend this idea to infinite sets. The sets A and B have the same cardinality if and only if there is a one-to-one correspondence from A to B. A set that is either finite or has the same cardinality as the set of natural numbers is called countable. A set that is not countable is called uncountable.

Cardinality Cardinality of set of natural numbers? An infinite set is countable if and only if it is possible to list the elements in a sequence (indexed by the positive integers). – Why? A one-to-one correspondence f can be expressed in terms of the sequence a1, a2, a3 ., where a1 f(1), a2 f(2), etc. – One-to-one correspondence for set of odd positive integers (in terms of positive integers)? f(n) 2n - 1






