Doc. g la colline des plaisirs D’après Vilfredo PARETO, Manuel
26 Slides618.50 KB
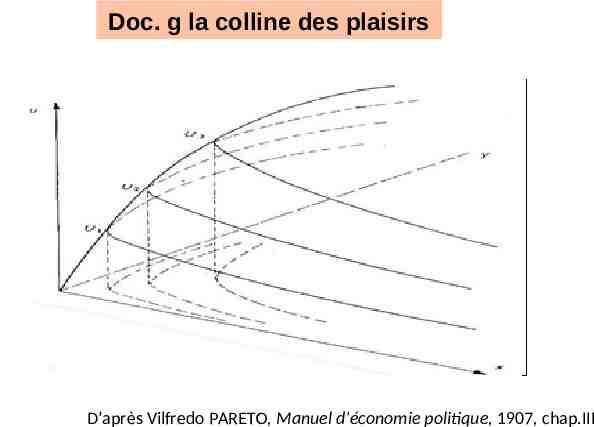
Doc. g la colline des plaisirs D’après Vilfredo PARETO, Manuel d’économie politique, 1907, chap.III

Doc. h l’axiomatique des préférences La relation de préférence s’écrit : A B : si le panier A est strictement préféré au panier B. A B : si le panier A est équivalent au panier B. Autrement dit, le consommateur est indifférent entre le panier A et le panier B A B : si le panier A est préféré au panier B. Autrement dit, A est strictement préféré ou équivalent à B. Cette relation de préférence est caractérisée par trois axiomes : - L’axiome de totalité : les consommateurs sont toujours capables de classer les paniers. Pour tout A et B, A B ou B A - L’axiome de transitivité : (A B et B C) A C - L’axiome de réflexivité : A A (bien sûr, en réalité on a même plus précisément A A) Ces axiomes font que les préférences constituent un pré-ordre complet, et qu’on peut alors représenter les préférences par une fonction d’utilité. D’après V. PARETO, Manuel d’économie politique, 1907

Les paniers de consommation Y YA XA X

Les courbes d’indifférence Y U3 U2 U1 X
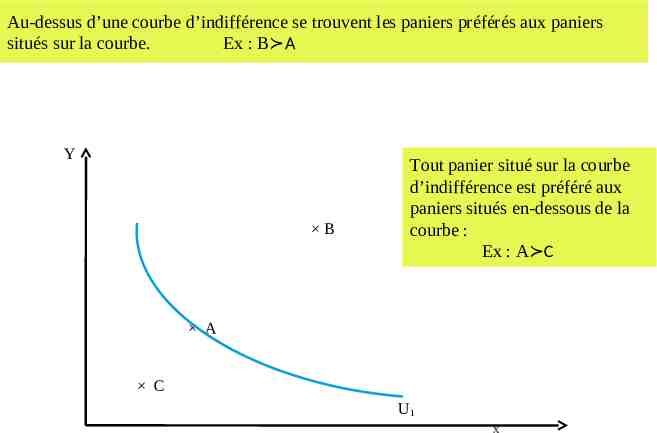
Au-dessus d’une courbe d’indifférence se trouvent les paniers préférés aux paniers situés sur la courbe. Ex : B A Y B Tout panier situé sur la courbe d’indifférence est préféré aux paniers situés en-dessous de la courbe : Ex : A C A C U1 X

Les courbes d’indifférence les plus éloignées de l’origine correspondent à des niveaux d’utilité plus élevés. U3 U2 U1 Y U3 U2 U1 X

Les courbes d’indifférence ne se croisent jamais : Y Démonstration par l’absurde : Comme A et B appartiennent à U, on a A B. Comme A et C appartiennent à V, on a A C Par transitivité, on a donc B C Pourtant B est situé au-dessus de V, ce qui donne B C A x B xC U V X

Les courbes d’indifférence sont décroissantes : Démonstration par l’absurde : Si A et B appartiennent à U, on a A B. Y U B Pourtant B est un panier mieux garni à la fois en bien X et en bien Y, ce qui viole l’hypothèse de non-satiété. A X

La convexité des courbes d’indifférence capture le goût pour la diversité, la « préférence pour les mélanges ». Les paniers A et B sont des paniers peu équilibrés. A comporte beaucoup de bien Y et peu de bien X. B comporte beaucoup de bien X et peu de bien Y. Y xA Tout panier qui est une combinaison linéaire de A et B est plus équilibré. C’est le cas du panier C. C est un panier plus diversifié que A. C Or, la convexité de la courbe d’indifférence assure que C A et C B B U1 X

Signification de la pente de la courbe d’indifférence : La valeur absolue de la pente de la courbe d’indifférence en un point (par exemple A) nous donne la quantité de bien Y que le consommateur est prêt à sacrifier pour garnir son panier d’une unité de bien X supplémentaire en restant au même niveau de satisfaction. Y C’est le taux marginal de substitution. Lorsqu’il dispose du panier A, le consommateur restera aussi satisfait s’il substitue une unité supplémentaire de bien X à une quantité de bien Y correspondant à la valeur absolue de la pente de la courbe d’indifférence. A U1 X

Quelle est la forme des courbes d’indifférence pour deux biens complémentaires ? Y U3 U2 U1 X

Quelle est la forme des courbes d’indifférence pour deux biens parfaitement substituables ? Y U3 U2 U1 X

Quelle est la forme des courbes d’indifférence lorsque X est un bien neutre ? Y U3 U2 U1 X

Doc. i la fonction d’utilité On appelle fonction d’utilité une fonction qui associe à un panier de biens de consommation l’utilité qu’il procure. C’est une fonction à plusieurs variables : elle compte autant de variables que de biens qui forment les paniers. Dans le cas où on étudie le choix d’un consommateur entre deux biens X et Y, la fonction d’utilité se note : U(X,Y) C’est une fonction à deux variables. Cette fonction permet de représenter les préférences d’un agent. Soient deux paniers A et B, correspondant respectivement aux quantités (X A, YA) et (XB, YB) Alors A B (XA, YA) (XB, YB) U(XA, YA) U(XB, YB)

Doc. i la fonction d’utilité (suite) Il s’agit pour étudier le choix du consommateur d’analyser les variations de l’utilité. Ces variations viennent des variations des quantités des biens consommées. L’utilité augmente lorsqu’on accroît la consommation de bien X, ou la consommation de bien Y. On note cette relation par la différentielle de la fonction d’utilité : U(X, Y) U(X, Y) dU(X, Y) dX dY U 'X (X, Y)dX U 'Y (X, Y)dY X Y dU : variation de l’utilité. dX : variation de la quantité de bien X. dY : variation de la quantité de bien Y.

Doc. i la fonction d’utilité (suite et fin) U(X, Y) U(X, Y) dU(X, Y) dX dY U 'X (X, Y)dX U 'Y (X, Y)dY X Y U(X, Y) U 'X (X, Y) X En termes économiques, c’est l’utilité marginale de X. En termes mathématiques, c’est la dérivée partielle de la fonction U par rapport à la variable X. U(X, Y) U 'X (X, Y) X En termes économiques, c’est l’utilité marginale de Y. En termes mathématiques, c’est la dérivée partielle de la fonction U par rapport à la variable Y. La dérivée partielle d’une fonction à plusieurs variables se définit de façon analogue à la dérivée d’une fonction à une seule variable : la dérivée partielle de la fonction U par rapport à la variable X est la dérivée par rapport à X lorsque Y est constant. Graphiquement, la dérivée partielle par rapport à X correspond à la pente de la colline des plaisirs lorsque X varie et que Y reste constant.

La contrainte budgétaire : R XPX YPY Y Avec R : revenu PX : prix du bien X PY : prix du bien Y Y R PX X PY La droite de budget délimite les possibilités de consommation, c’est-à-dire les paniers de consommation accessibles au consommateur R/Py R/PX X

Effet d’une hausse du revenu de R à R’ Y R’/Py R/Py R/PX R’/PX X

Effet d’une diminution du prix du bien X de PX à P’X Y R/Py R/PX R/P’XX

Le panier de consommation optimale C’est le panier de consommation qui maximise l’utilité totale d’un consommateur sous sa contrainte budgétaire. Y Pourquoi correspond-il au point (X*,Y*) ? Y* Umax X* X

Doc. j le programme du consommateur Le consommateur dépense son revenu de manière à maximiser son utilité, soit : max U(X, Y) X, Y s.c. . PX X PY Y R Si on fait l’hypothèse que le consommateur dépense l’intégralité de son revenu, la contrainte budgétaire est saturée, on a alors : PX X PY Y R Y R PX X PY Le programme du consommateur se réécrit alors : maxU(X, X R PX X ) PY

Doc. j le programme du consommateur (suite) R PX X maxU(X, ) X PY Cette fonction d’utilité est continue et dérivable en chacune de ces variables, elle atteint son maximum quand sa dérivée est nulle, c’est à dire : * PX U Y (X * , Y * ) d * R PX X * * U(X , ) U X (X , Y ) 0 dX PY PY U X (X * , Y * ) PX U X (X * , Y * ) PX U Y (X * , Y * ) PY U Y (X * , Y * ) PY On a écrit ici la condition de premier ordre du programme du consommateur. On a retrouvé la 2nde loi de Gossen. 0

La révélation des préférences Y Le choix du panier de consommation A révèle qu’il est préféré à tout panier de consommation B faisant partie des possibilités de consommation. Il s’agit d’une révélation directe des préférences. A est directement révélé comme préféré à B. xA xB X

La révélation indirecte des préférences Y Si le consommateur choisit B suite à une variation de la contrainte budgétaire, on a une révélation directe des préférences par rapport à B (zone hachurée), mais aussi une révélation indirecte des préférences par rapport à A. A B et B C A C. Ainsi, A est indirectement révélé comme préféré à C. xA xB xC X

A quel âge devient-on un consommateur rationnel ? Une expérience a soumis des jeunes à des choix successifs entre différents paniers composés de paquets de chips et de briques de jus. On peut ensuite vérifier ci ses choix successifs sont conformes à la rationalité de la microéconomie du consommateur Le taux de choix rationnels : 25 % à 7 ans 60 % à 11 ans 65 % à 21 ans W. HARBAUGH, K. KRAUSE & T. BERRY, « GARP for Kids : On the Development of Rational Choice Behavior », American Economic Review, 2001. http://harbaugh.uoregon.edu/Papers/GARPforKids.pdf

Doc. k La méthode du Lagrangien Soit le programme du consommateur : max U(X, Y) s.c. PX X PY Y R . X, Y On appelle Lagrangien associé à ce programme la fonction : L(X,Y, λ) U(X, Y) λ(PX X PY Y R) . Le Lagrangien permet d’introduire la contrainte dans la fonction-objectif avec une certaine pénalité λ. λ est le multiplicateur de Lagrange. On peut alors montrer que la résolution du programme du consommateur revient à maximiser le Lagrangien, ce qui implique les conditions de premier ordre suivantes : L(X * ,Y * ,λ * ) U X (X * , Y * ) λ * PX 0 X L(X * ,Y * ,λ * ) U Y (X * , Y * ) λ * PY 0 Y L(X * ,Y * ,λ * ) (PX X PY Y R) 0 λ Dans les deux premières équations, on reconnaît les conditions d’optimum du premier rang, alors que la troisième est équivalente à la contrainte budgétaire : PX X PY Y R L’intérêt de la méthode du Lagrangien n’apparaît pas immédiatement dans le cas d’une fonction d’utilité à deux variables, mais elle simplifie le calcul lorsqu’on a un plus grand nombre de variables. De plus, le multiplicateur de Lagrange λ a une interprétation intéressante. λ donne une approximation de la variation de U(X, Y) lorsqu’on augmente d'une unité le revenu R. Ainsi, λ 2 signifie que l’utilité augmenterait approximativement de 2 si on augmentait le revenu d’une unité. Le multiplicateur de Lagrange convertit donc les unités monétaire de la contrainte budgétaire en unité d’utilité compatibles avec U(X, Y)






