Data Structures & Algorithms Network Flow Richard Newman based on
66 Slides1.21 MB

Data Structures & Algorithms Network Flow Richard Newman based on book by R. Sedgewick

Network Flow Problems Weighted, digraph G, or network May have cost per unit flow for edges May have maximum flow per edge May have max production rates May have required consumption rate per sink

Distribution Problems Merchandise distribution – Sources with production rates – Sinks with consumption rates – Distribution centers Input rate output rate – Channels with maximum rate and unit cost for distribution
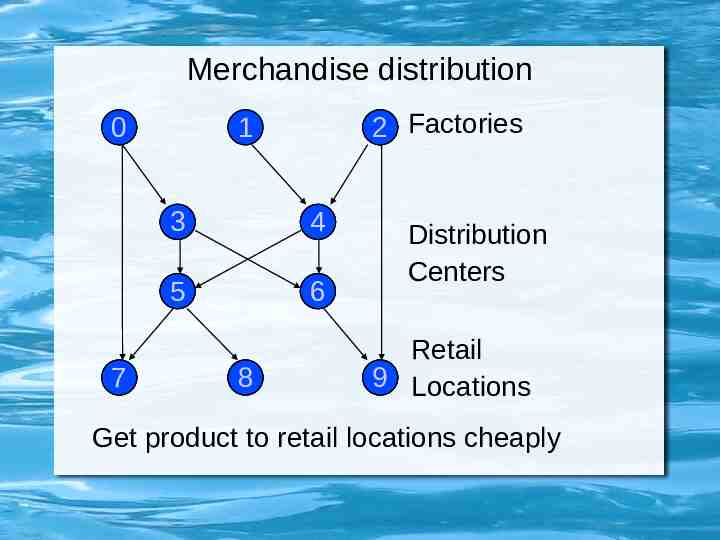
Merchandise distribution 0 7 1 72 3 4 5 6 8 Factories Distribution Centers Retail 9 Locations Get product to retail locations cheaply

Transportation Problems Communications – Max total data rate between a source and sink – Cheapest way to move a given amount of data from s to t Traffic flow – Minimize evacuation time – Minimize total cost
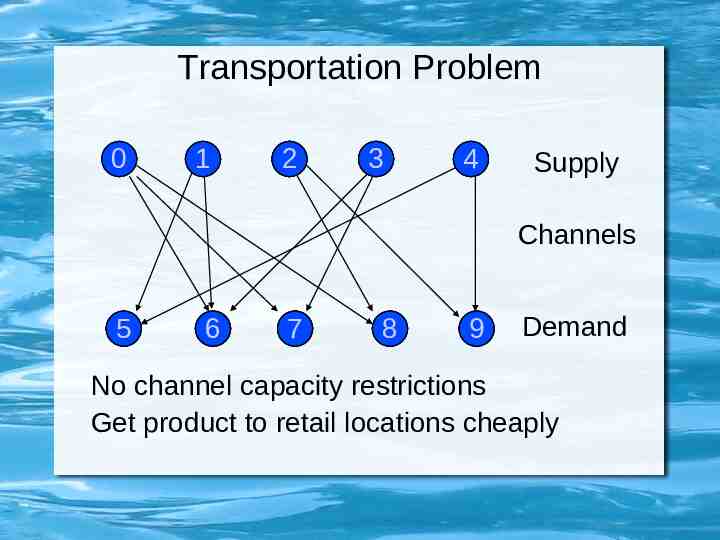
Transportation Problem 0 1 72 3 4 Supply Channels 5 6 7 8 9 Demand No channel capacity restrictions Get product to retail locations cheaply

Matching Problems Job placement – Interviews job offers – Maximize number of placements Min-distance point matching – Two sets A and B of N points each – Find set of N segments matching an element from A with one from B that has lowest cost
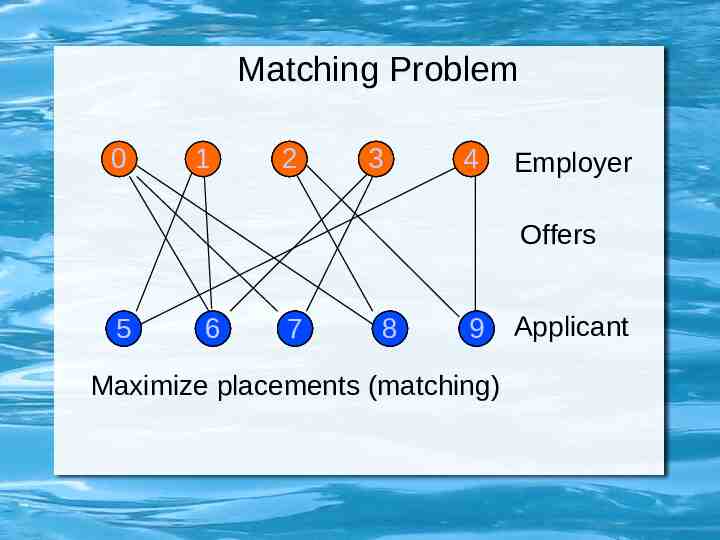
Matching Problem 0 1 72 3 4 Employer Offers 5 6 7 8 9 Maximize placements (matching) Applicant

Cut Problems Network reliability – What is minimum number of lines that must be cut to disconnect two switches? Supply line cutting – What is the minimum supply line destruction required to ensure no troops get supplies?
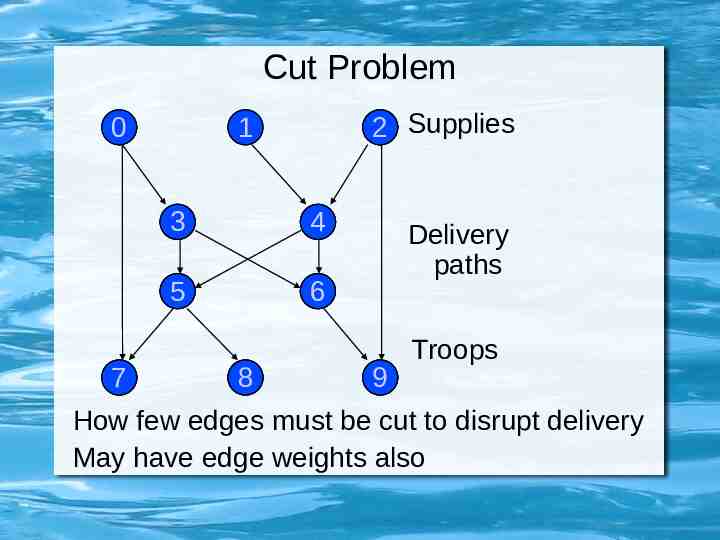
Cut Problem 0 7 1 72 3 4 5 6 8 Supplies Delivery paths 9 Troops How few edges must be cut to disrupt delivery May have edge weights also

Network Flow Problems Generic problems Maxflow – What is maximum flow between s and t? Mincost-flow – What is cheapest cost way to achieve a particular flow?

Network Flow Flow Networks Maxflow Algorithms Maxflow Reductions Mincost Flows Network Simplex Algorithm

Flow Networks Defn 22.1: A network with a single source and a single sink is an s-t network

Flow Networks Defn 22.2: A flow network is an s-t network with positive edge weights, called capacities. A flow in a flow network is a set of non-negative edge weights called edge flows satisfying: No edge flow exceeds capacity In flow out flow for interior nodes
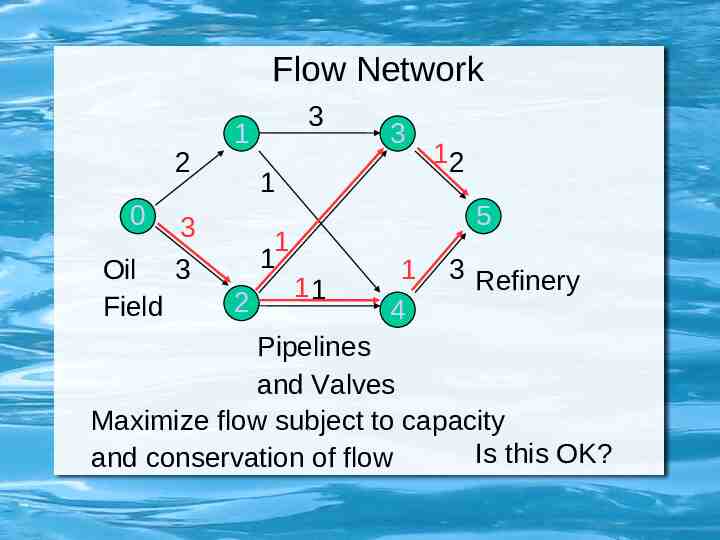
Flow Network 2 0 1 3 1 3 Oil 3 Field 3 1 1 2 12 5 11 1 4 3 Refinery Pipelines and Valves Maximize flow subject to capacity Is this OK? and conservation of flow
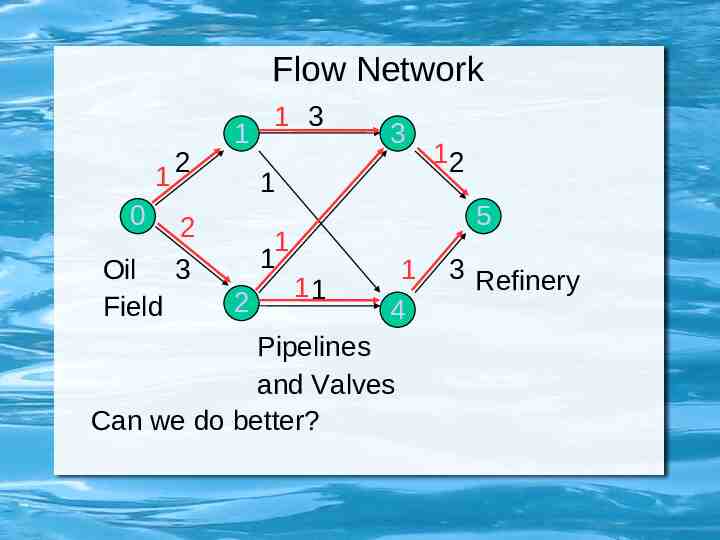
Flow Network 1 0 2 1 3 1 2 Oil 3 Field 1 3 1 1 2 12 5 11 1 4 Pipelines and Valves Can we do better? 3 Refinery
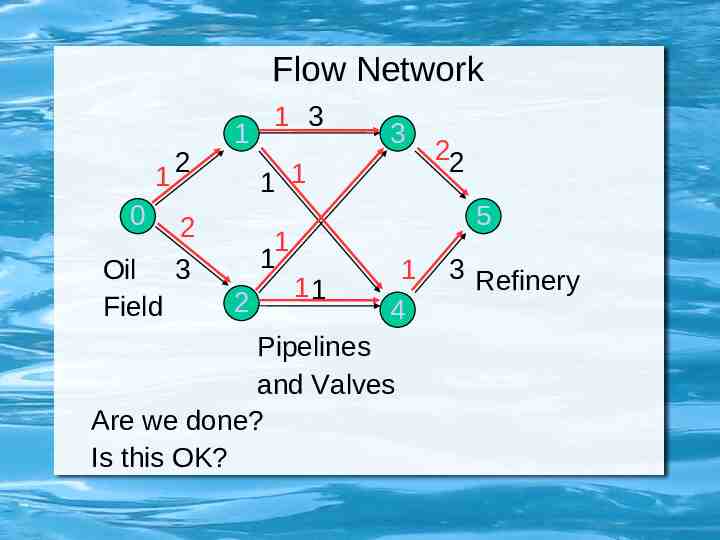
Flow Network 1 0 2 1 3 1 1 2 Oil 3 Field 1 3 1 1 2 22 5 11 1 4 Pipelines and Valves Are we done? Is this OK? 3 Refinery
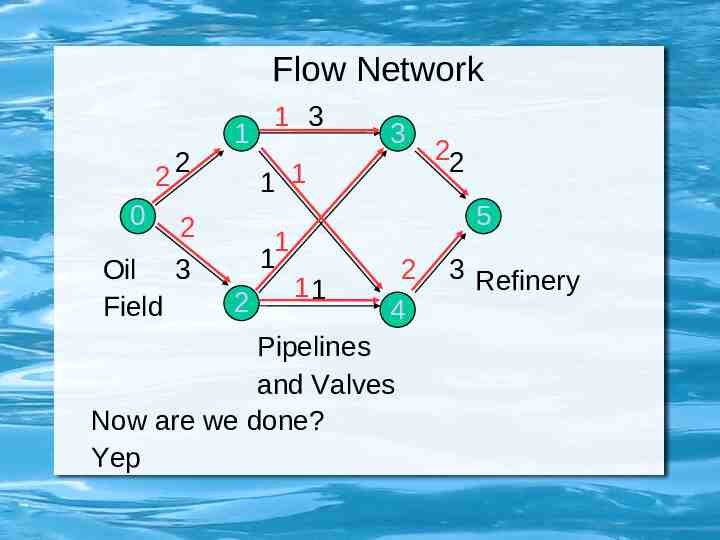
Flow Network 2 0 2 1 3 1 1 2 Oil 3 Field 1 3 1 1 2 22 5 11 2 4 Pipelines and Valves Now are we done? Yep 3 Refinery

Flow Network Sum of flows into a node is called inflow Sum of flows out of a node is called outflow Conservation of flow: except for source and sink, inflow outflow Feasible flow obeys constraints (max flow and conservation of flow)

Flow Network Set outflow from sink to zero Set inflow to source to zero Outflow of source inflow of sink This is called network's value

Maximum Flow Given an s-t network, find a flow such that no other flow from s to t has a larger value. A flow like this is called a maxflow. Problem of finding one is called the maxflow problem.

Augmenting Path Maximum Flow First algorithm like this due to Ford and Fulkerson Iteratively: Find a feasible path from s to t Find the max residual capacity on it Saturate the path by adding flow along it equal to the minimum residual capacity
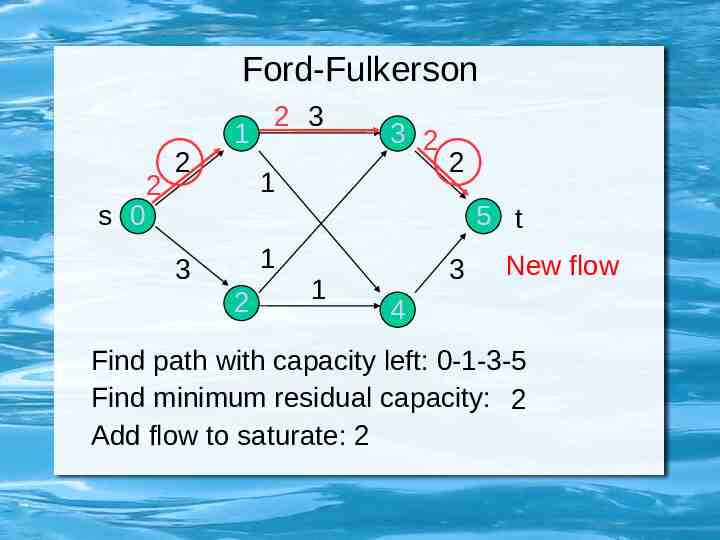
Ford-Fulkerson s 0 2 2 1 2 3 3 2 1 2 5 t 1 3 2 1 3 New flow 4 Find path with capacity left: 0-1-3-5 Find minimum residual capacity: 2 Add flow to saturate: 2
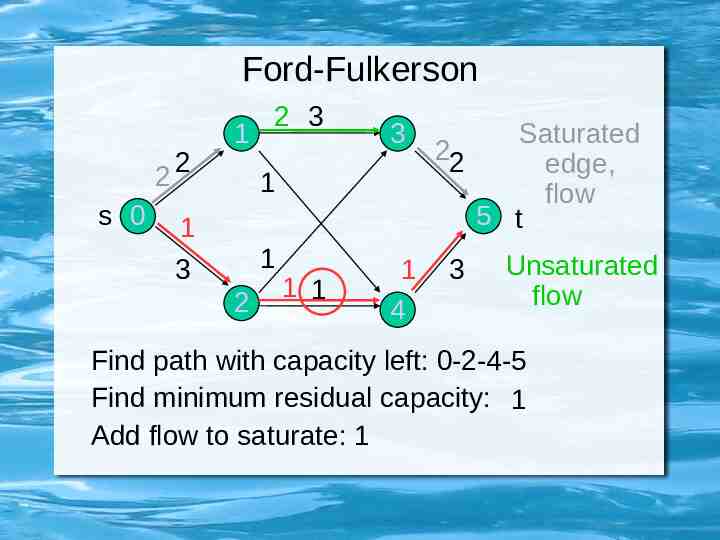
Ford-Fulkerson 2 s 0 2 1 2 3 3 1 1 1 3 2 1 1 1 4 Saturated 22 edge, flow 5 t 3 Unsaturated flow Find path with capacity left: 0-2-4-5 Find minimum residual capacity: 1 Add flow to saturate: 1
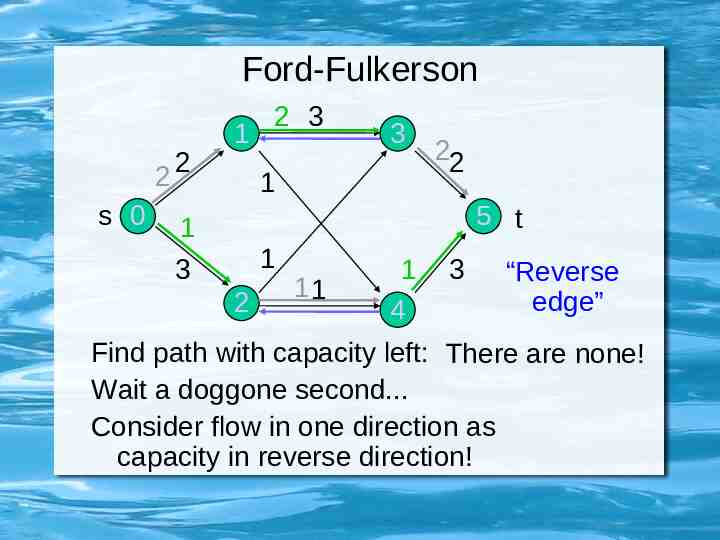
Ford-Fulkerson 2 s 0 2 1 2 3 3 1 22 5 t 1 1 3 2 11 1 4 3 “Reverse edge” Find path with capacity left: There are none! Wait a doggone second. Consider flow in one direction as capacity in reverse direction!
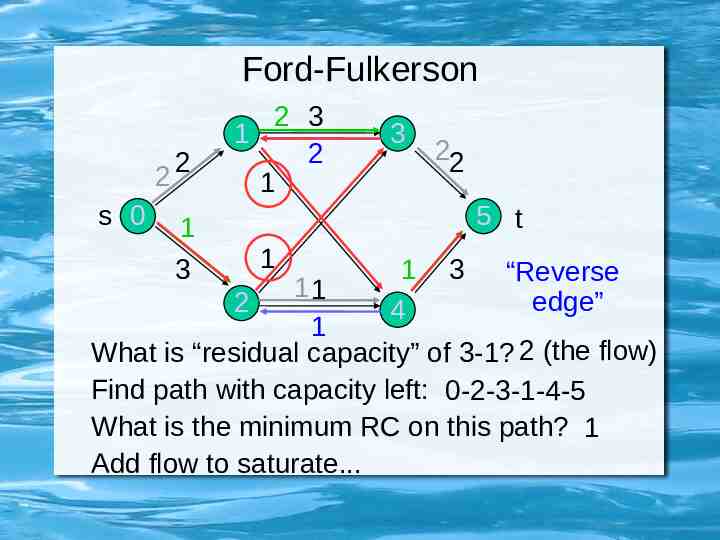
Ford-Fulkerson 2 s 0 2 1 3 2 3 1 2 1 3 22 5 t 1 1 4 3 “Reverse edge” 11 2 1 What is “residual capacity” of 3-1? 2 (the flow) Find path with capacity left: 0-2-3-1-4-5 What is the minimum RC on this path? 1 Add flow to saturate.
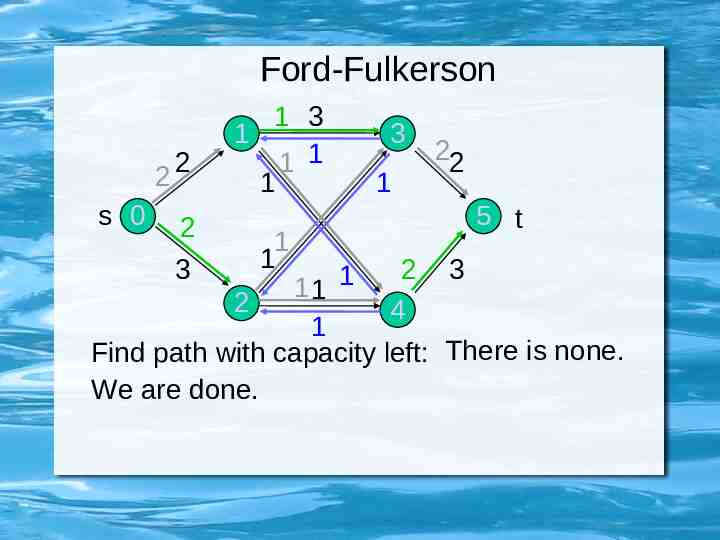
Ford-Fulkerson 2 s 0 2 2 3 1 3 1 1 1 1 1 1 3 1 22 5 t 1 2 4 3 11 2 1 Find path with capacity left: There is none. We are done.
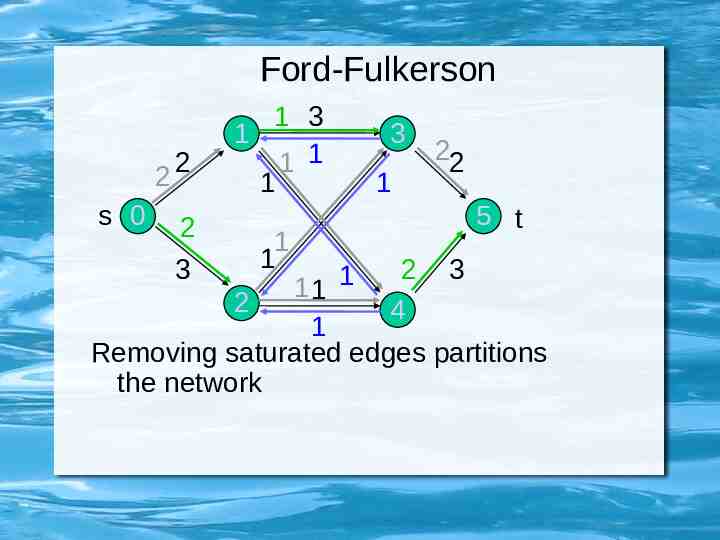
Ford-Fulkerson 2 s 0 2 2 3 1 3 1 1 1 1 1 1 3 1 22 5 t 1 2 4 3 11 2 1 Removing saturated edges partitions the network
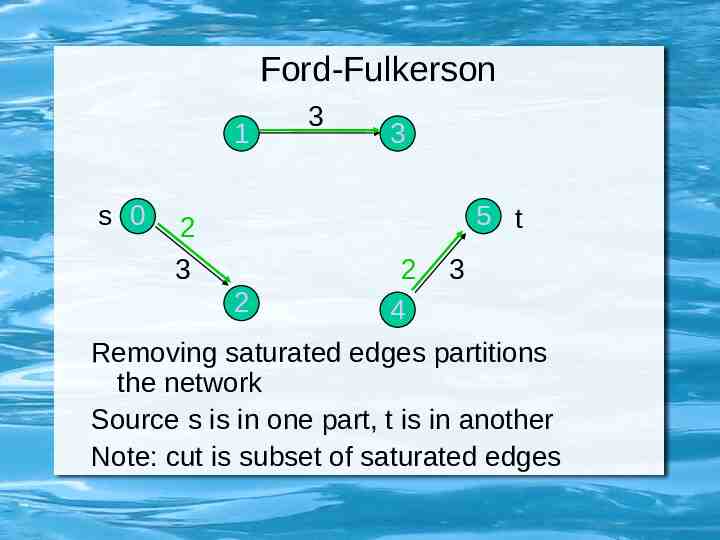
Ford-Fulkerson 1 s 0 3 3 5 t 2 3 2 2 4 3 Removing saturated edges partitions the network Source s is in one part, t is in another Note: cut is subset of saturated edges

s-t Cut Defn. 22.3: An s-t cut is a cut that places node s in one of its sets and node t in the other. Its capacity is the sum of its edge weights. The flow across an s-t cut is the sum of the flows across its s-t edges, less the sum of the flows across its t-s edges.

MinCut Problem Given an s-t network, find an s-t cut such that the capacity of no other cut is smaller. We call this a mincut. Maxflow-mincut theorem – min cut capacity and maxflow value are equal

Residual Network Given flow network G and a flow F, the residual network R for the flow has the same nodes, and one or two edges in R for each edge in the original: for edge (v,w) in G, let f be the flow and c be the capacity. If f c, include (v,w) with capacity c-f; if 0 include (w,v) with capacity f.

Residual Network If flow is 0, then the original edge with original capacity is used For positive flows, decrease capacity by the flow (unless the residual capacity is zero – the edge is saturated – remove the edge) For positive flows, add a reverse directed edge with the flow as its capacity (can reduce flow that much).
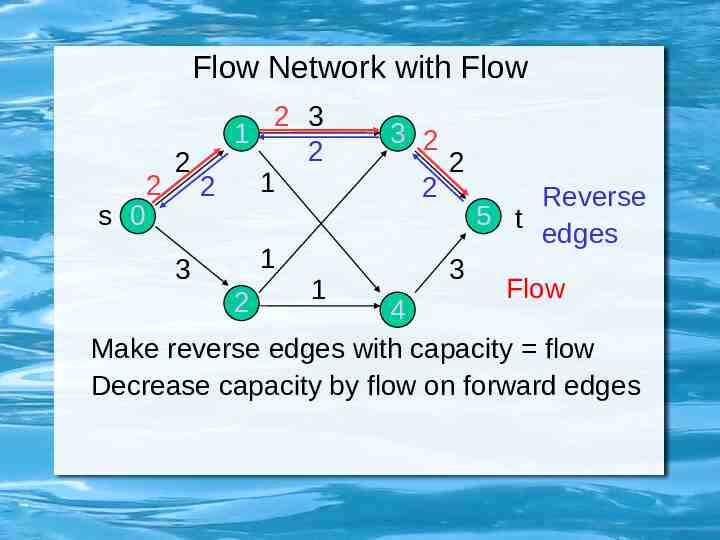
Flow Network with Flow s 0 2 3 1 2 2 1 2 2 1 3 2 1 3 2 2 2 Reverse 5 t edges 3 Flow 4 Make reverse edges with capacity flow Decrease capacity by flow on forward edges
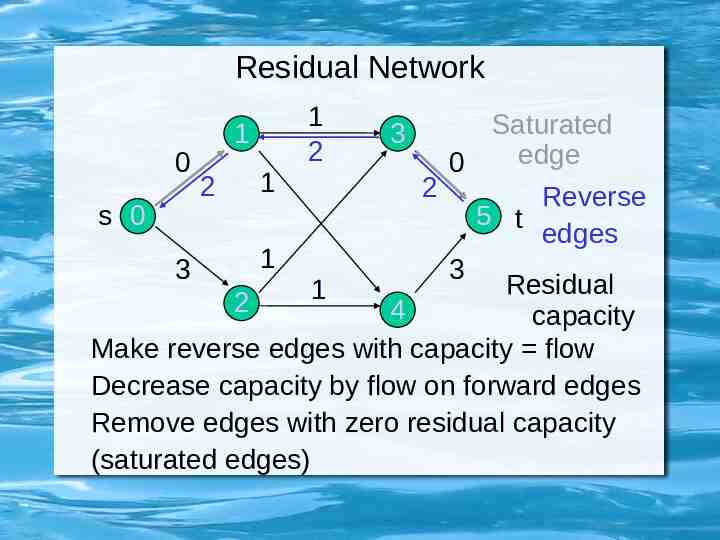
Residual Network 1 2 Saturated edge 0 0 1 2 2 Reverse s 0 5 t edges 1 3 3 Residual 1 2 4 capacity Make reverse edges with capacity flow Decrease capacity by flow on forward edges Remove edges with zero residual capacity (saturated edges) 1 3
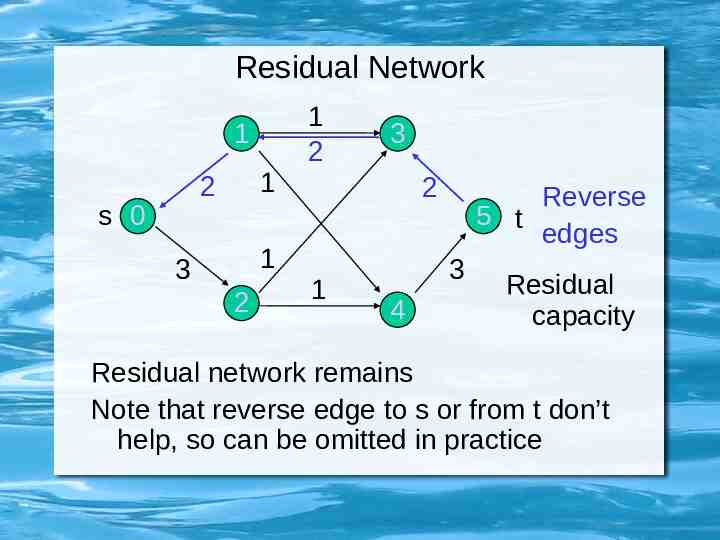
Residual Network 1 1 2 s 0 1 3 2 1 2 3 2 1 Reverse 5 t edges 3 4 Residual capacity Residual network remains Note that reverse edge to s or from t don’t help, so can be omitted in practice

Variants on Ford-Fulkerson Shortest Augmenting Path Measured by number of edges Build “layer graph” – like BFS Which nodes can be reached by 1 edge, then by 2 edges, etc. Stop when t is reached and add flow to saturate edge on path to t

Variants on Ford-Fulkerson Maximum Flow Augmenting Path Measured by max flow along path Pick edges that give max flow to next layer Take max of (min flow along path to predecessor u, capacity (u,v)) to find max flow to v through u at that layer

Ford-Fulkerson Complexity Prop. 22.6: Let M be the maximum edge capacity in G. The number of augmenting paths needed by any implementation of F-F is at most VM. Every AP adds at least one unit of flow to every cut; any cut has at most V edges; hence the algorithm must terminate after VM passes since any cut must be saturated by then.

Ford-Fulkerson Complexity Cor: The time required to find a maxflow is O(VEM), which is O(V2M) for sparse networks. Linear (in edges) graph search per pass. Need extra lg V factor if using priority queue fringe implementation Actual performance is quite good

Ford-Fulkerson Complexity Prop. 22.7: The number of augmenting paths needed in the shortest augmenting path F-F algo is at most VE/2.

Ford-Fulkerson Complexity The length of the APs monotone nondecreasing. Every AP has a critical edge that is saturated in its pass. Each time edge e is the critical edge, the AP must be at least 2 hops longer. The longest path has V edges

Ford-Fulkerson Complexity Prop. 22.7 (again): The number of augmenting paths needed in the shortest augmenting path F-F algo is at most VE/2. Cor: The time required to find a maxflow in a sparse network is O(V3) O(E) time per pass, VE/2 passes, and if G is sparse, E is O(V).

Ford-Fulkerson Complexity Prop. 22.8: The number of augmenting paths needed in the maximal augmenting path F-F algo is at most 2E lg M. Cor: The time required to find a maxflow in a sparse network is O(V2 lg M lg V)

Network Flow Flow Networks Maxflow Algorithms Maxflow Reductions Mincost Flows Network Simplex Algorithm

Maxflow in General Networks Maximize the total outflow from sources in a network. (Zero by convention if no sources or sinks) Multiple sources Multiple sinks Still need feasible flows!

Maxflow in General Networks Prop. 22.14: The maxflow in general networks is equivalent to the maxflow problem for general networks. The general case subsumes the special case of s-t networks. Add dummy source connected to all sources and dummy sink to all sinks by high-capacity edges

Vertex-capacity Constraints Given a flow network, find a maxflow satisfying additional constraints that the flow through each node v must not exceed the capacity of that node.

Vertex-capacity Constraints Prop. 22.15: The maxflow with node capacity problem is equivalent to maxflow problem. Setting node capacity high subsumes the special case of s-t networks. Node capacity can be set to max of in-capacity and out-capacity (sum of in- and out-edge capacities, resp.)

Vertex-capacity Constraints Prop. 22.15: The maxflow with node capacity problem is equivalent to maxflow problem. Split each node into in-part and outpart, with all in-edge to in-part and all out-edge from out-part Make edge from in-part to out-part with edge capacity node capacity in original problem

Maxflow in Acyclic Networks Maximize the total outflow from sources in an acyclic network. Seems like it might be easier But NO! Easy transformation from any network to acyclic network V nodes - 2V 2 nodes E edges - E 3V edges

Maxflow in General Networks Prop. 22.16: The maxflow in acyclic networks is equivalent to the maxflow problem for general networks. The construction allows a mincut in original to reveal a mincut in the transformed version, and vice versa, with transformed cut values. p427

Maxflow in Undirected Networks Prop. 22.17: The maxflow in undirected networks reduces to the maxflow problem for s-t networks. Just make two directed edges in the s-t network for every edge in the undirected network Make both edge capacities equal to the corresponding edge capacity in the undirected network

Maxflow in Undirected Networks Note that we did not say equivalent! It remains possible that finding maxflows in undirected networks is easier than finding them in directed networks.

Feasible Flow Given a flow network G, assign a weight to each node, interpreted as supply if positive, and demand if negative. A flow is feasible if it obeys flow constraints AND if the difference between the outflow sum and inflow sum for each node v v’s weight Finding a feasible flow is FF problem

Feasible Flow Prop. 22.18: The feasible flow problem reduces to maxflow Make flow network with V more nodes. For supply nodes, make the new node a source with edge weight the same as the node weight For demand nodes make the new node a sink with edge capacity -weight

Feasible Flow Prop. 22.18: The feasible flow problem reduces to maxflow Feasible flow exists in original network iff maxflow in constructed flow network saturates all edges between sources and companions and all edges between sinks and companions

Max-cardinality Bipartite Matching Given a bipartite graph G, find a set of edges of maximum cardinality such that each vertex is connected to at most one other vertex. A.k.a. Bipartite Matching Problem Direct solution by trying all possibilities results in combinatorial explosion!

Max-cardinality Bipartite Matching Prop. 22.19: Bipartite matching reduces to the maxflow problem. Make edges directed from set A to set B nodes Add two dummy nodes s and t Add edges from s to each node in A Add edges from each node in B to t Assign capacity 1 to all edges

Edge-Connectivity Prop. 22.20: The minimum number of edges whose removal disconnects two nodes in a digraph is equal to the number of edge-disjoint paths between the two nodes. Define a flow network with the same nodes and edges, with capacities all 1. The capacity of any s-t cut is equal to the cut’s cardinality

Connectivity Problems Edge connectivity Node connectivity Digraphs Undirected graphs Hence 4 problems Can do reductions .

Edge-Connectivity Prop. 22.21: The time required to determine the edge-connectivity of an undirected graph G is O(E2) Compute min cut in corresponding s-t network with unit capacity edges. Edge connectivity for G is the minimum over all s-t pairs Note we only have to use a minimal degree vertex as s – faster

Network Flow Flow Networks Maxflow Algorithms Maxflow Reductions Mincost Flows Network Simplex Algorithm

Mincost Flows Flow network has cost also associated with each edge Defn 22.8: Flow cost of an edge is the product of the flow and the edge cost. The cost of a flow is the sum of the flow costs of that flow’s edges.

Mincost Flows Mincost Maxflow Find maxflow with minimum flow cost Mincost Feasible Flow Find feasible flow with minimum cost Prop 22.22: The mincost feasible flow and the mincost maxflow problems are equivalent.

Network Flow Flow Networks Maxflow Algorithms Maxflow Reductions Mincost Flows Network Simplex Algorithm






