Cryptography CS 111 — Lecture 19 Prof. Amit Sahai
58 Slides987.50 KB

Cryptography CS 111 -- Lecture 19 Prof. Amit Sahai

Last Time We saw examples of search problems that we believe Computers can’t solve quickly. In computer-science terminology: NP All Search Problems P Problems we can solve quickly We believe that P NP, i.e. not every search problem can be solved quickly on a computer. (Otherwise life would be too good.) But we don’t know how to prove it!
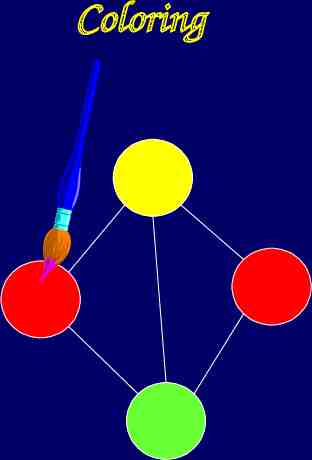
Coloring

Last Time (cont.) We saw that the Coloring Problem is as hard as any search problem: In particular, we can reduce solving any search problem to finding a valid coloring for some collection of circles! So, if we could solve Coloring quickly, then P NP That’s why we believe Coloring can’t be solved quickly by any computer. We call such problems NP-Complete.

Other Hard Problems? There are other problems besides NP-Complete Problems that we also believe are hard. How can we be sure? We can’t. But humanity has been trying to solve certain mathematical problems for centuries. It seems reasonable to assume that nobody will figure out how to solve them soon.

Cryptography Why do we care so much about hard problems? Because sometimes we want to make things hard. Protecting Privacy, Authenticity Want to make it hard for adversaries to: Steal our credit cards Impersonate us Etc.

Cryptography Science of making things hard for adversaries Cryptography Today: we’ll learn the basic principles used to protect credit cards online and much more. Beautiful and mathematically sophisticated field This is your professor’s main area of research.
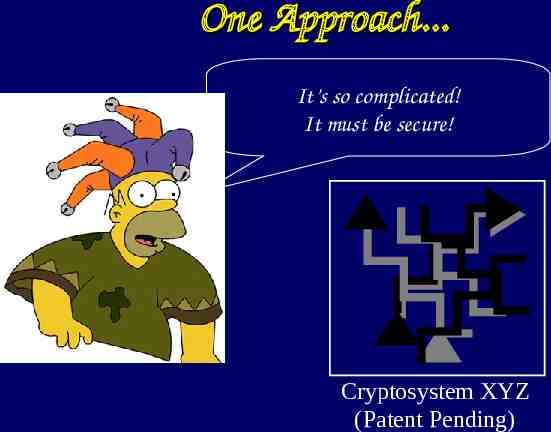
One Approach. It’s so complicated! It must be secure! Cryptosystem XYZ (Patent Pending)

One Approach. Cryptosystem XYZ Broken 2 Days After Release!

One Approach. Unfortunately, this approach is often used in real life. This is one of the reasons why you hear about so many security systems being broken! Examples: DVD encryption, Cell phones in Europe (GSM), many many more

Our Approach. We’ll of course take a much more disciplined approach. We’ll use the theory of hard search problems and our notion of reducing one problem to another: We want to show that if you break our security system, you will have to solve some of the world’s greatest unsolved problems first!

Encryption The most basic problem in Cryptography is Encryption: Private Message m Alice Bob
Encryption The most basic problem in Cryptography is Encryption: Private Message m Bob Alice Eve the eavesdropper
Encryption The most basic problem in Cryptography is Encryption: Encrypted Message E(m) Bob Alice Eve the eavesdropper
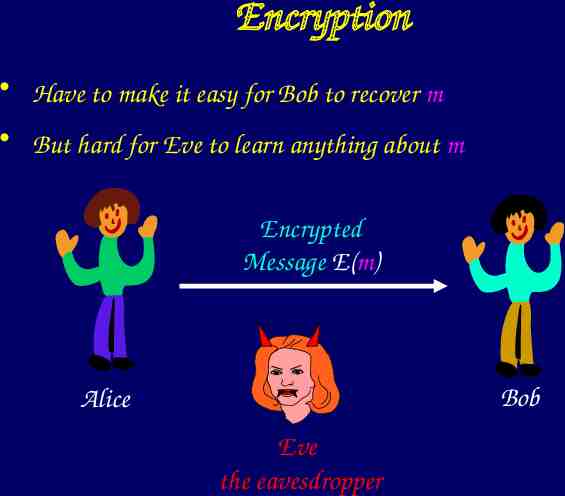
Encryption Have to make it easy for Bob to recover m But hard for Eve to learn anything about m Encrypted Message E(m) Bob Alice Eve the eavesdropper

Public-Key Cryptography [Diffie-Hellman 1976] Bob’s Public Key Bob’s Secret Key Bob Everybody knows Bob’s published Public Key. Only Bob knows his secret key.

Public-Key Encryption Encrypted Message E(m) Alice Alice uses Bob’s public key to encrypt m. Bob uses his secret key to recover (decrypt) m. Bob

Public-Key Encryption Encrypted Message E(m) Alice Eve the eavesdropper Bob Alice and Eve both know Bob’s public key. Eve must not be able to “break” the encryption even though she knows the public key.

Basic Math Review Let’s recall some basic mathematics: A number p is called prime if its only factors are 1 and itself. Examples:

Basic Math Review Let’s recall some basic mathematics: A number p is called prime if its only factors are 1 and itself. Examples: 2, 3, 5, 7, 11, 13, 17, 19,

Basic Math Review Let’s recall some basic mathematics: A number p is called prime if its only factors are 1 and itself. Examples: 2, 3, 5, 7, 11, 13, 17, 19, There are lots of prime numbers. Fact: It is known how to check quickly if a number is prime or not. So, to find a big prime number, we can just keep generating large random numbers until we find a prime.

Basic Math Review Given two primes p and q, it is easy to multiply them together: N pq But given N, how do you find p and q quickly? i.e. how do you factor N? Easy for small numbers (e.g. 6 or 35). For centuries, mathematicians have been trying to find ways to factor large numbers quickly. No one knows how! Factoring a 10,000 digit N would take centuries on the fastest computer in existence!

Basic Math & Crypto We want to make it so that if Eve the eavesdropper breaks our system, she would have to factor a very large number. We’ll (almost) do that.

Modular Arithmetic Ordinary Arithmetic: -4 -3 -2 -1 0 1 2 3 4

Modular Arithmetic Ordinary Arithmetic: -4 -3 -2 -1 Arithmetic Modulo N: 0 1 2 3 N 0 1 (N – 1) 2 (N – 2) (N – 3) 3 4

Modular Arithmetic Example: Arithmetic Modulo 12 (like Arithmetic on time) 3 11 (Modulo 12) 2 – 4 (Modulo 12) 5 * 4 (Modulo 12) 4 * 3 (Modulo 12)

Modular Arithmetic Example: Arithmetic Modulo 12 (like Arithmetic on time) 3 11 (Modulo 12) 2 2 – 4 (Modulo 12) 5 * 4 (Modulo 12) 4 * 3 (Modulo 12)

Modular Arithmetic Example: Arithmetic Modulo 12 (like Arithmetic on time) 3 11 (Modulo 12) 2 2 – 4 (Modulo 12) 10 5 * 4 (Modulo 12) 4 * 3 (Modulo 12)

Modular Arithmetic Example: Arithmetic Modulo 12 (like Arithmetic on time) 3 11 (Modulo 12) 2 2 – 4 (Modulo 12) 10 5 * 4 (Modulo 12) 8 4 * 3 (Modulo 12)

Modular Arithmetic Example: Arithmetic Modulo 12 (like Arithmetic on time) 3 11 (Modulo 12) 2 2 – 4 (Modulo 12) 10 5 * 4 (Modulo 12) 8 4 * 3 (Modulo 12) 0

The RSA Encryption Scheme [Rivest Shamir Adleman 1978] Bob picks two large primes p and q, and computes: N pq Fact: Because Bob knows p and q, he can pick numbers e and d such that: For all m: ed (m ) m (Modulo N) Bob’s Public Key will be e, N Bob’s secret key will be d

The RSA Encryption Scheme Fact: Because Bob knows p and q, he can pick numbers e and d such that: For all m: ed (m ) m (Modulo N) To Encrypt a message m, Alice computes: E(m) me (Modulo N)

The RSA Encryption Scheme Fact: Because Bob knows p and q, he can pick numbers e and d such that: For all m: ed (m ) m (Modulo N) To Encrypt a message m, Alice computes: E(m) me (Modulo N) To Decrypt, Bob computes: m E(m)d (Modulo N)

The RSA Encryption Scheme To Encrypt a message m, Alice computes: E(m) me (Modulo N) The only known way to compute m from E(m) involves factoring N. For Eve to break this system, she would have to solve a longstanding open problem in Mathematics. This is probably the most widely used Public-Key Encryption Scheme in the world.
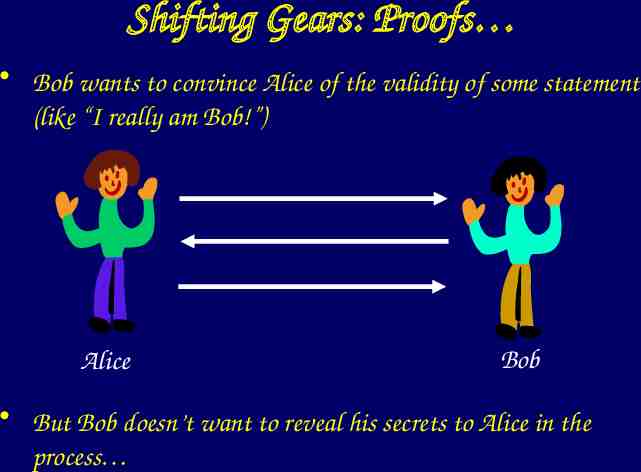
Shifting Gears: Proofs Bob wants to convince Alice of the validity of some statement (like “I really am Bob!”) Alice Bob But Bob doesn’t want to reveal his secrets to Alice in the process

Zero-Knowledge Proofs [Goldwasser Micali Rackoff 85] What is the least amount of information Bob can reveal, while still convincing Alice? Amazingly, it is possible for Bob to convince Alice of something without revealing any information at all! How can that be?

Magic Tricks Magic tricks are like zero-knowledge proofs: Good magic tricks reveal nothing about how they work. What makes a magic trick good?

A Magic Trick Two balls: Purple and Red, otherwise identical Blindfolded Magician You give a random ball to magician

A Magic Trick (cont.) Magician tells you the color! Magician proves he can distinguish balls blindfolded. You learn nothing except this. Abracadabra, Goobedy goo! It is Red! Wow! He’s so cool!

A Magic Trick (cont.) You knew exactly what magician was going to do. And he did it! Since you knew to begin with, you could not have learned anything new! It’s Red! I knew he would say that.

Zero Knowledge What it means: Alice “knows” what is going to happen. CS-speak: Alice can simulate it herself! Simulation Abracadabra, Goobedy goo! It is Red!

Another Magic Trick Magician asks you to think of either “Apple” or “Banana” Magician then gives you a sealed box.

Mind Reading You tell Magician what you were thinking. I was thinking of a banana.

Mind Reading (cont.) Magician tells you to open box, and read piece of paper in box. Magician proves he can predict what you will say. Banana How did he do that!!

Mind Reading (cont.) Again, you knew what was going to happen. Zero-Knowledge Simulation Banana I was thinking of a banana.

Mind Reading (cont.) But why was it convincing? Because Magician committed to his guess before you told him.

Cryptographic Commitment Public Key Encryption Scheme To commit to a string x, I send y E(x). To open the commitment, I reveal my secret key. Commitment is secret. And I can’t change my mind about x once I’ve sent the encryption.

NP-Completeness Remember we can reduce any search problem to Coloring.

NP-Completeness (cont.) “y is an encryption of a valid tax return” reduction

ZK Proof for Coloring Input: Collection of circles. Magician Knows: Coloring using R, B, G First, Magician picks random permutation : R,B,G R,B,G , and applies to coloring:
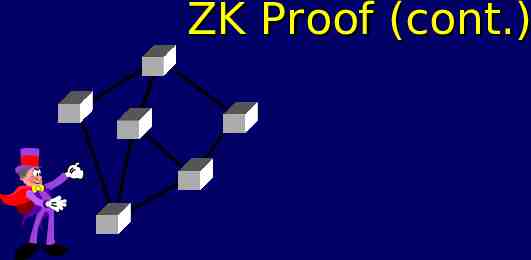
ZK Proof (cont.)
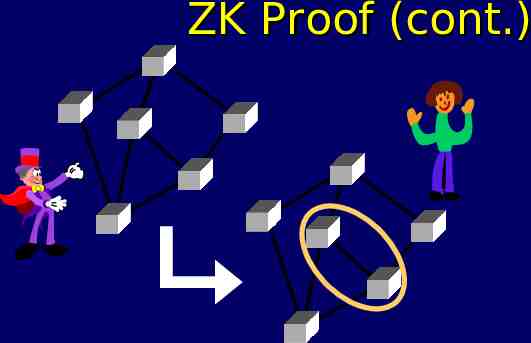
ZK Proof (cont.)
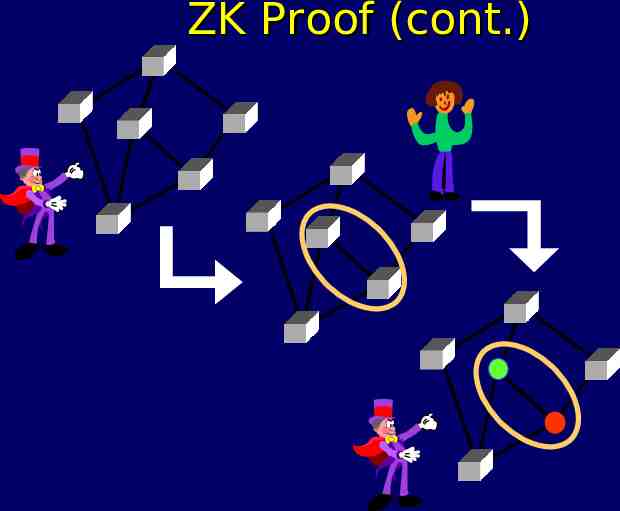
ZK Proof (cont.)

ZK Proof: Analysis Suppose NO valid coloring exists. Then at least one pair of connected circles where colors equal. Alice catches Magician cheating with probability at least 1/n2. Repeat protocol 100 n2 times, Alice catches Magician cheating almost always!
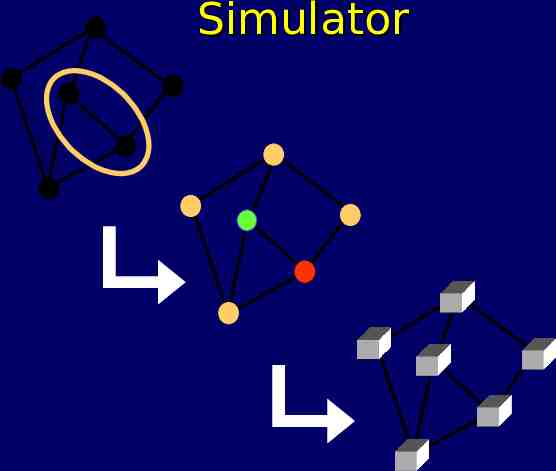
Simulator
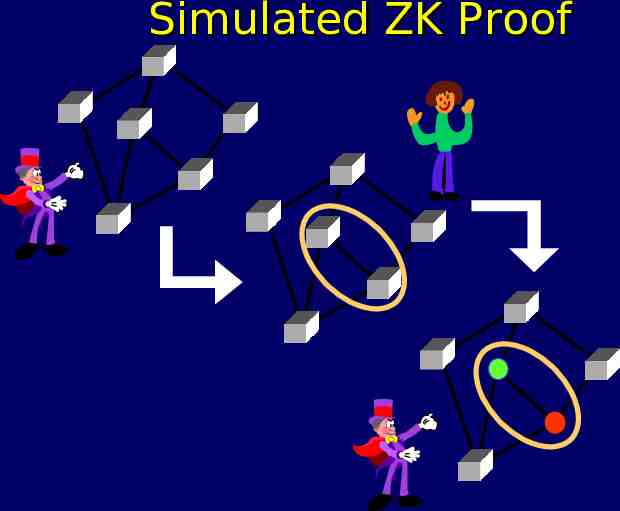
Simulated ZK Proof

ZK Proof: Analysis (cont.) Only difference between real & simulated: In real life, commitments are to valid coloring. In simulator, commitments are to invalid coloring. But commitments are secret, by security of encryption scheme. Simulator output and real life are indistinguishable.

Wrap-up Today we saw some examples illustrating techniques from modern cryptography: Encryption Zero Knowledge Proofs Next Time: Discussions on Computer Music & Intellectual Property.






