Information Security — Part II Asymmetric Ciphers Frank
56 Slides1.03 MB

Information Security -- Part II Asymmetric Ciphers Frank Yeong-Sung Lin Information Management Department National Taiwan University

Outline Introduction to information security Introduction to public-key cryptosystems RSA Diffie-Hellman key exchange ECC Mutual trust – Key management – User authentication YSL Information Security -- Public-Key Cryptography 2

Areas Considered by Info. Security Secrecy (Confidentiality): keep information unrevealed Authentication: determine the identity of whom you are talking to Nonrepudiation: make sure that someone cannot deny the things he/she had done Integrity control: make sure the message you received has not been modified Availability: make sure the resource be available for authorized personnel when needed YSL Information Security -- Public-Key Cryptography 3

Essential Concepts for Info. Security Risk management – threats, vulnerabilities, assets, damages and probabilities – balancing acts – all cryptosystems may be compromised (trade-off between overhead and expected time span of protection) YSL Notion of chains (Achilles' heel) Notion of buckets (products, policies, processes and people) Defense in-depth Average vs. worst cases Backup, restoration and contingency plans Information Security -- Public-Key Cryptography 4

A Number of Interesting Ciphers Chinese poems Clubs and leather stripes Invisible ink (steganography in general) Books Code books Enigma XOR (can be considered as an example of symmetric cryptosystems) Ej/vu3z8h96 Scramblers (physical and application layers) YSL Information Security -- Public-Key Cryptography 5

Principles of Public-Key Cryptosystems YSL Information Security -- Public-Key Cryptography 6

Principles of Public-Key Cryptosystems (cont’d) Requirements for PKC – easy for B (receiver) to generate KUb and KRb – easy for A (sender) to calculate C EKUb(M) – easy for B to calculate M DKRb(C) DKRb(EKUb(M)) – infeasible for an opponent to calculate KRb from KUb – infeasible for an opponent to calculate M from C and KUb – (useful but not necessary) M DKRb(EKUb(M)) EKUb(DKRb(M)) (true for RSA and good for authentication) YSL Information Security -- Public-Key Cryptography 7

Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 8

Principles of Public-Key Cryptosystems (cont’d) The idea of PKC was first proposed by Diffie and Hellman in 1976. Two keys (public and private) are needed. The difficulty of calculating f -1 is typically facilitated by – factorization of large numbers – resolution of NP-completeness – calculation of discrete logarithms High complexity confines PKC to key management and signature applications YSL Information Security -- Public-Key Cryptography 9
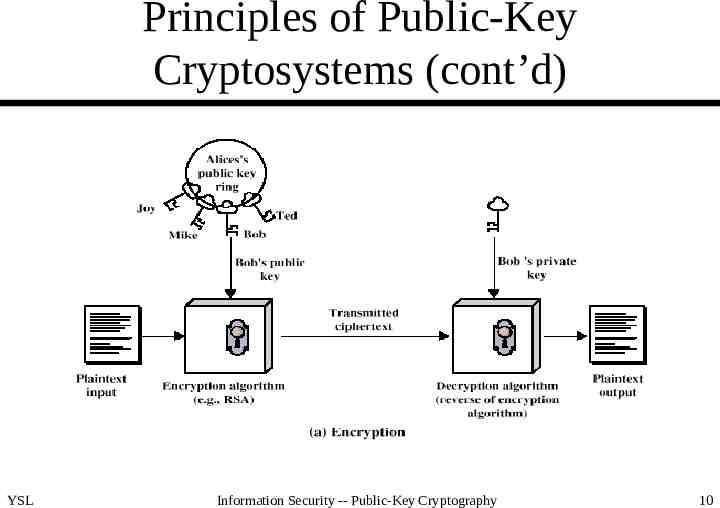
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 10
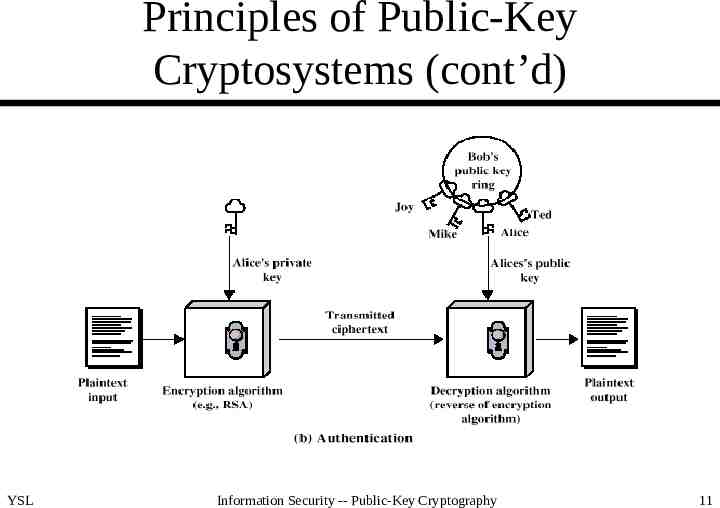
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 11

Principles of Public-Key Cryptosystems (cont’d) Comparison between conventional and public-key encryption Conventional Encryption Public-Key Encryption Needed to Work: Needed to Work: 1. The same algorithm with the same key 1. One algorithm is used for encryption is used for encryption and decryption. and decryption with a pair of keys, one for encryption and one for decryption. 2. The sender and receiver must share the 2. The sender and receiver must each have algorithm and the key. one of the matched pair of keys (not the same one). Needed for Security: Needed for Security: 1. The key must be kept secret. 1. One of the two keys must be kept secret. 2. It must be impossible or at least 2. It must be impossible or at least impractical to decipher a message if no impractical to decipher a message if no other information is available. other information is available. 3. Knowledge of the algorithm plus 3. Knowledge of the algorithm plus one samples of ciphertext must be of the keys plus samples of ciphertext insufficient to determine the key. must be insufficient to determine the other key. YSL Information Security -- Public-Key Cryptography 12

Principles of Public-Key Cryptosystems (cont’d) Applications for PKC – encryption/decryption – digital signature – key exchange Algorithm RSA Diffie-Hellman DSS YSL Encryption/Decryption Yes No No Digital Signature Yes No Yes Information Security -- Public-Key Cryptography Key Exchange Yes Yes No 13
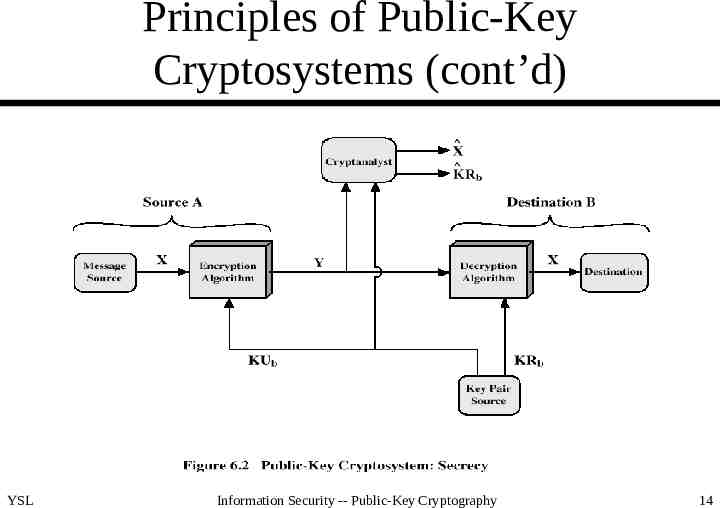
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 14
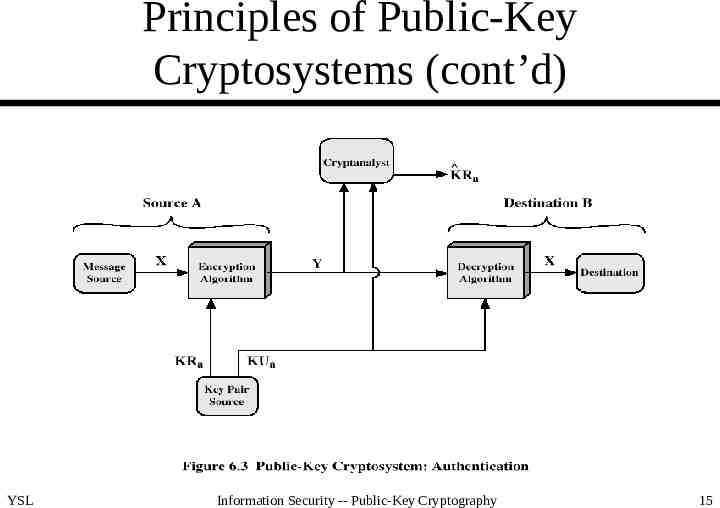
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 15
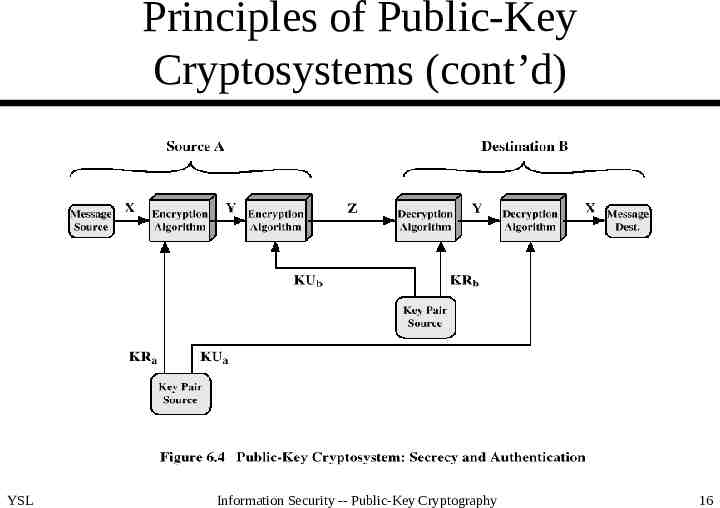
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 16

The RSA Algorithm Developed by Rivest, Shamir, and Adleman at MIT in 1978 First well accepted and widely adopted PKC algorithm Security based on the difficulty of factoring large numbers Patent expired in 2001 YSL Information Security -- Public-Key Cryptography 17
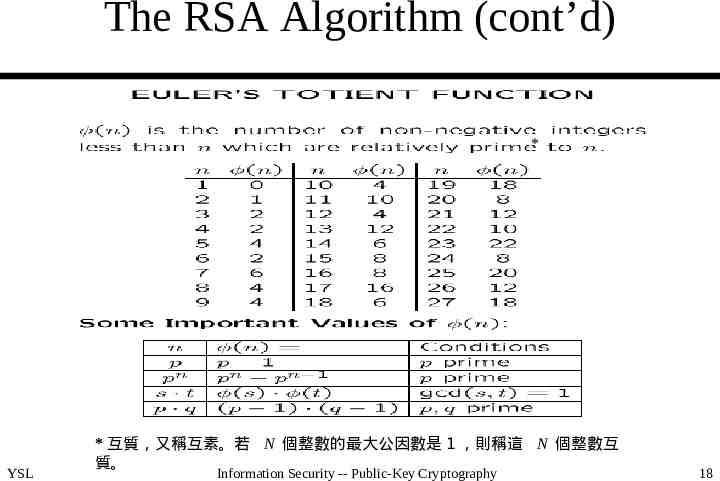
The RSA Algorithm (cont’d) * YSL * 互質,又稱互素。若 N 個整數的最大公因數是 1 ,則稱這 N 個整數互 質。 Information Security -- Public-Key Cryptography 18

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 19

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 20

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 21

The RSA Algorithm (cont’d) 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 281 283 293 307 311 313 317 331 337 347 349 449 457 461 463 467 479 487 491 499 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1063 1069 1087 1091 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 79 83 89 97 887 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 Primes under 2000 YSL Information Security -- Public-Key Cryptography 22
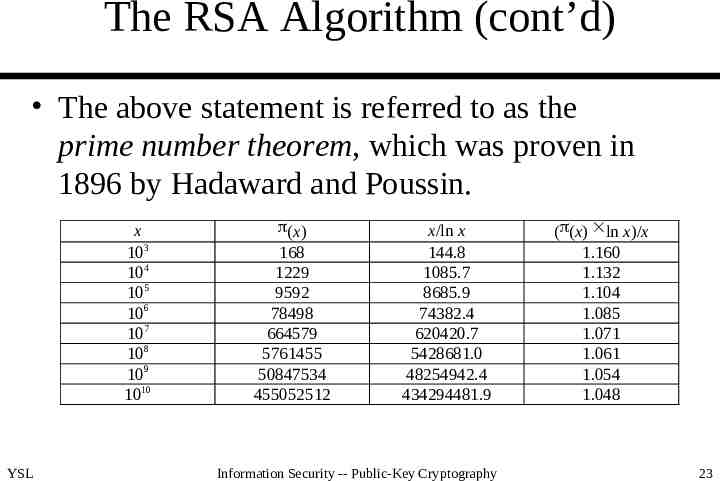
The RSA Algorithm (cont’d) The above statement is referred to as the prime number theorem, which was proven in 1896 by Hadaward and Poussin. x 103 104 105 106 107 108 109 1010 YSL (x) 168 1229 9592 78498 664579 5761455 50847534 455052512 x/ln x 144.8 1085.7 8685.9 74382.4 620420.7 5428681.0 48254942.4 434294481.9 Information Security -- Public-Key Cryptography ( (x) ln x)/x 1.160 1.132 1.104 1.085 1.071 1.061 1.054 1.048 23

The RSA Algorithm (cont’d) Whether there exists a simple formula to generate prime numbers? An ancient Chinese mathematician conjectured that if n divides 2n - 2 then n is prime. For n 3, 3 divides 6 and n is prime. However, for n 341 11 31, n dives 2341 - 2. Mersenne suggested that if p is prime then Mp 2p - 1 is prime. This type of primes are referred to as Mersenne primes*. Unfortunately, for p 11, M11 211 -1 2047 23 89. YSL Information Security -- Public-Key Cryptography 24

The RSA Algorithm (cont’d) *In mathematics, a Mersenne number is a positive integer that is one less than a power of two: Mn 2n – 1. Some definitions of Mersenne numbers require that the exponent n be prime. A Mersenne prime is a Mersenne number that is prime. As of September 2008, only 46 Mersenne primes are known; the largest known prime number (243,112,609 1) is a Mersenne prime, and in modern times, the largest known prime has almost always been a Mersenne prime. Like several previously-discovered Mersenne primes, it was discovered by a distributed computing project on the Internet, known as the Great Internet Mersenne Prime Search (GIMPS). It was the first known prime number with more than 10 million digits. YSL Information Security -- Public-Key Cryptography 25

The RSA Algorithm (cont’d) Fermat conjectured that if Fn 22n 1, where n is a non-negative integer, then Fn is prime. When n is le ss than or equal to 4, F0 3, F1 5, F2 17, F3 2 57 and F4 65537 are all primes. However, F5 42 94967297 641 6700417 is not a prime number. n2 - 79n 1601 is valid only for n 80. There are an infinite number of primes of the form 4n 1 or 4n 3. There is no simple way so far to gererate prime nu mbers. YSL Information Security -- Public-Key Cryptography 26

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 27

The RSA Algorithm (cont’d) Prime gap: displacement between two consecutive prime numbers – 0 the smallest – unbounded from above – n! 2 (devisable by 2), n! 3 (devisable by 3, n! 4 (devisable by 4), , n! n (devisable by n) are not prime YSL Information Security -- Public-Key Cryptography 28

The RSA Algorithm (cont’d) Format’s Little Theorem (to be proven later): If p is prime and a is a positive integer not divisible by p, then a p-1 1 mod p. Example: a 7, p 19 72 49 11 mod 19 74 121 7 mod 19 78 49 11 mod 19 716 121 7 mod 19 a p-1 718 716 2 7 11 1 mod 19 YSL Information Security -- Public-Key Cryptography 29

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 30

The RSA Algorithm (cont’d) YSL A M ip for a non-negative integer i. A M jq for a non-negative integer j. From the above two equations, ip jq. Then, i kq. Consequently, A M ip M kpq. Q.E.D. (quod erat demonstrandum) Information Security -- Public-Key Cryptography 31
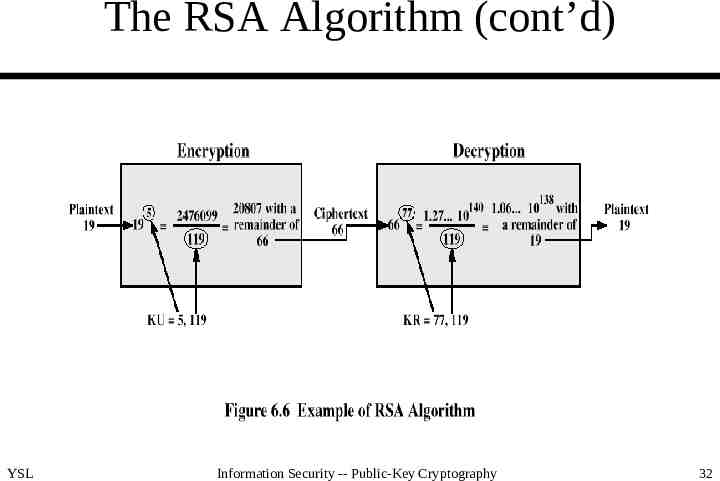
The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 32

The RSA Algorithm (cont’d) Example 1 – – – – Select two prime numbers, p 7 and q 17. Calculate n p q 7 17 119. Calculate Φ(n) (p-1)(q-1) 96. Select e such that e is relatively prime to Φ(n) 96 and less than Φ(n); in this case, e 5. – Determine d such that d e 1 mod 96 and d 96.The correct value is d 77, because 77 5 385 4 96 1. YSL Information Security -- Public-Key Cryptography 33

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 34

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 35

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 36

The RSA Algorithm (cont’d) Key generation – determining two large prime numbers, p and q – selecting either e or d and calculating the other Probabilistic algorithm to generate primes – [1] Pick an odd integer n at random. – [2] Pick an integer a n (a is clearly not divisible by n) at random. – [3] Perform the probabilistic primality test, such as Miller-Rabin. If n fails the test, reject the value n and go to [1]. – [4] If n has passed a sufficient number of tests, accept n; otherwise, go to [2]. YSL Information Security -- Public-Key Cryptography 37

The RSA Algorithm (cont’d) How may trials on the average are required to find a prime? – from the prime number theory, primes near n are spaced on the average one every (ln n) integers – even numbers can be immediately rejected – for a prime on the order of 2200, about (ln 2200)/2 70 trials are required To calculate e, what is the probability that a random number is relatively prime to Φ(n)? About 0.6. YSL Information Security -- Public-Key Cryptography 38

The RSA Algorithm (cont’d) For fixed length keys, how many primes can be chosen? – for 64-bit keys, 264/ln 264 - 263/ln 263 2.05 1017 – for 128- and 256-bit keys, 1.9 1036 and 3.25 1074, respectively, are available For fixed length keys, what is the probability that a randomly selected odd number a is prime? – for 64-bit keys, 2.05 1017/(0.5 (264 - 263)) 0.044 (expectation value: 1/0.044 23) – for 128- and 256-bit keys, 0.022 and 0.011, respectively YSL Information Security -- Public-Key Cryptography 39

The RSA Algorithm (cont’d) The security of RSA – brute force: This involves trying all possible private keys. – mathematical attacks: There are several approaches, all equivalent in effect to factoring the product of two primes. – timing attacks: These depend on the running time of the decryption algorithm. YSL Information Security -- Public-Key Cryptography 40

The RSA Algorithm (cont’d) To avoid brute force attacks, a large key space is required. To make n difficult to factor – p and q should differ in length by only a few digits (both in the range of 1075 to 10100) – both (p-1) and (q-1) should contain a large prime factor – gcd(p-1,q-1) should be small – should avoid e n and d n1/4 YSL Information Security -- Public-Key Cryptography 41

The RSA Algorithm (cont’d) To make n difficult to factor (cont’d) – p and q should best be strong primes, where p is a strong prime if there exist two large primes p1 and p2 such that p1 p-1 and p2 p 1 there exist four large primes r1, s1, r2 and s2 such that r1 p1-1, s1 p1 1, r2 p2-1 and s2 p2 1 – e should not be too small, e.g. for e 3 and C M3 mod n, if M3 n then M can be easily calculated YSL Information Security -- Public-Key Cryptography 42
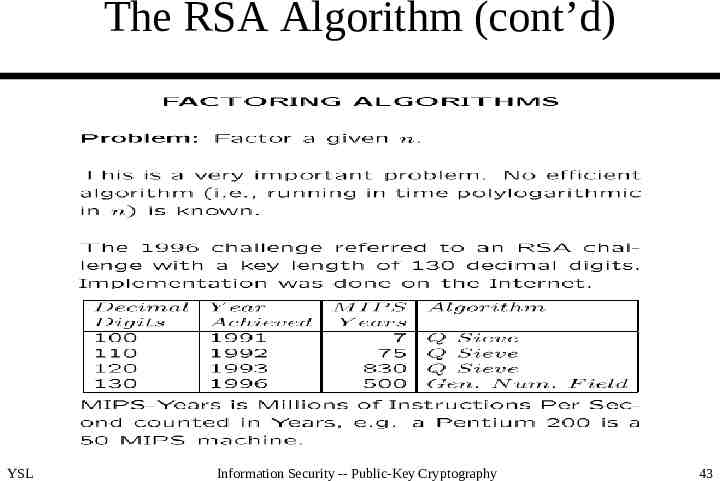
The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 43

The RSA Algorithm (cont’d) Major threats – the continuing increase in computing power (100 or even 1000 MIPS machines are easily available) – continuing refinement of factoring algorithms (from QS to GNFS and to SNFS) YSL Information Security -- Public-Key Cryptography 44
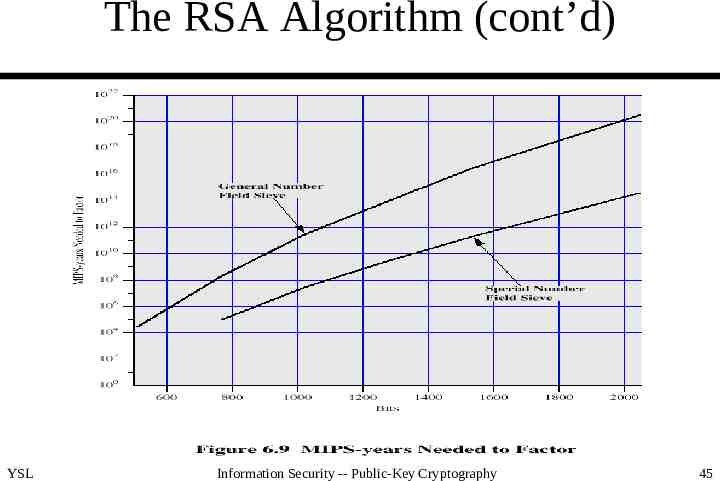
The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 45

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 46

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 47

Diffie-Hellman Key Exchange First public-key algorithm published Limited to key exchange Dependent for its effectiveness on the difficulty of computing discrete logarithm YSL Information Security -- Public-Key Cryptography 48

Diffie-Hellman Key Exchange (cont’d) Define a primitive root of of a prime number p as one whose powers generate all the integers from 1 to p-1. If a is a primitive root of the prime number p, then the numbers a mod p, a2 mod p, , ap-1 mod p are distinct and consist of the integers from 1 to p-1 in some permutation. Not every number has a primitive root. For example, 2 is a primitive root of 5, but 4 is not. YSL Information Security -- Public-Key Cryptography 49

Diffie-Hellman Key Exchange (cont’d) For any integer b and a primitive root a of prime number p, one can find a unique exponent i such that b ai mod p, where 0 i (p-1). The exponent i is referred to as the discrete logarithm, or index, of b for the base a, mod p. This value is denoted as inda,p(b) (dloga,p(b)). YSL Information Security -- Public-Key Cryptography 50

Diffie-Hellman Key Exchange (cont’d) YSL Information Security -- Public-Key Cryptography 51

Diffie-Hellman Key Exchange (cont’d) Example: q 97 and a primitive root a 5 is selected. XA 36 and XB 58 (both 97). YA 536 50 mod 97 and YB 558 44 mod 97. K (YB) X mod 97 4436 mod 97 75 mod 97. A K (YA) X mod 97 5058 mod 97 75 mod 97. B 75 cannot easily be computed by the opponent. YSL Information Security -- Public-Key Cryptography 52

Diffie-Hellman Key Exchange (cont’d) How the algorithm works X K (Y B ) ( X B mod ( X B ) B X A ( X A ) ( X A X (Y A ) YSL X mod A B X mod mod X q q) B mod X A mod q mod q q q mod q X q) mod A B q Information Security -- Public-Key Cryptography 53
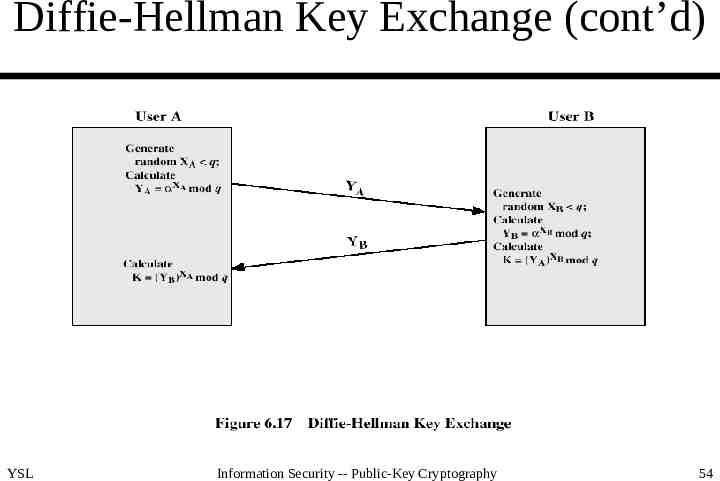
Diffie-Hellman Key Exchange (cont’d) YSL Information Security -- Public-Key Cryptography 54

Diffie-Hellman Key Exchange (cont’d) q, a, YA and YB are public. To attack the secrete key of user B, the opponent must compute XB inda,q(YB). [YB aX mod q.] The effectiveness of this algorithm therefore depends on the difficulty of solving discrete logarithm. B YSL Information Security -- Public-Key Cryptography 55
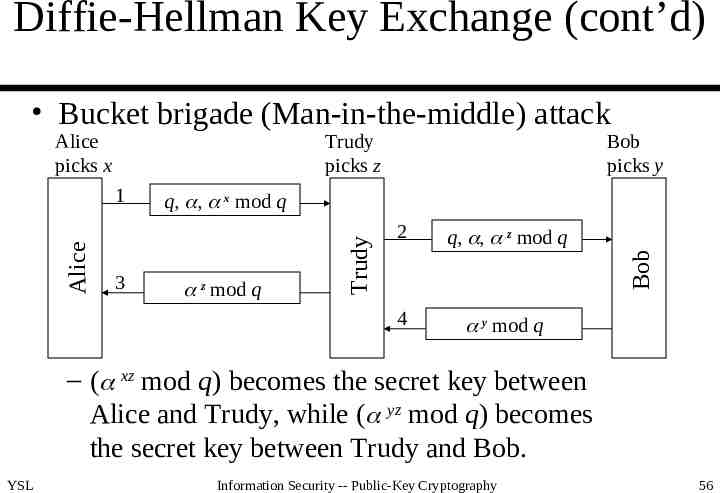
Diffie-Hellman Key Exchange (cont’d) Bucket brigade (Man-in-the-middle) attack Alice picks x Trudy picks z z mod q 2 q, , z mod q 4 y mod q Bob 3 q, , x mod q Trudy Alice 1 Bob picks y – ( xz mod q) becomes the secret key between Alice and Trudy, while ( yz mod q) becomes the secret key between Trudy and Bob. YSL Information Security -- Public-Key Cryptography 56






