CSE 541 – Interpolation Roger Crawfis

CSE 541 - Interpolation Roger Crawfis

Taylor’s Series and Interpolation Taylor Series interpolates at a specific point: – The function – Its first derivative – It may not interpolate at other points. We want an interpolant at several f(c)’s. February 6, 2023 OSU/CIS 541 2

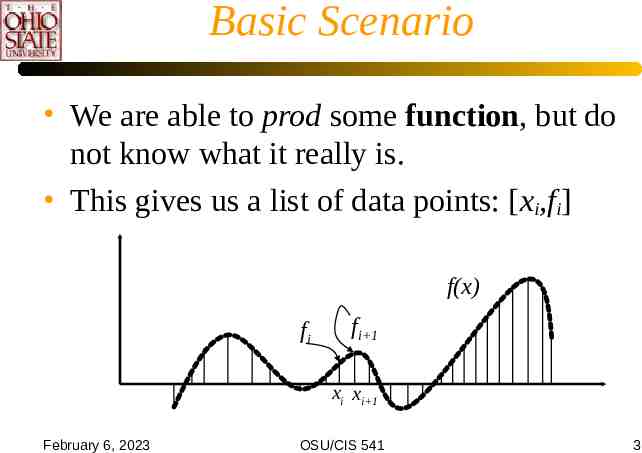
Basic Scenario We are able to prod some function, but do not know what it really is. This gives us a list of data points: [xi,fi] f(x) fi fi 1 xi xi 1 February 6, 2023 OSU/CIS 541 3

Interpolation & Curve-fitting Often, we have data sets from experimental/observational measurements – Typically, find that the data/dependent variable/output varies – As the control parameter/independent variable/input varies. Examples: Classic gravity drop: location changes with time Pressure varies with depth Wind speed varies with time Temperature varies with location Scientific method: Given data identify underlying relationship Process known as curve fitting: February 6, 2023 OSU/CIS 541 4

Interpolation & Curve-fitting Given a data set of n 1 points (xi,yi) identify a function f(x) (the curve), that is in some (well-defined) sense the best fit to the data Used for: – Identification of underlying relationship (modelling/prediction) – Interpolation (filling in the gaps) – Extrapolation (predicting outside the range of the data) February 6, 2023 OSU/CIS 541 5

Interpolation Vs Regression Distinctly different approaches depending on the quality of the data Consider the pictures below: extrapolate interpolate extrapolate Pretty confident: there is a polynomial relationship Little/no scatter Want to find an expression that passes exactly through all the points February 6, 2023 OSU/CIS 541 Unsure what the relationship is Clear scatter Want to find an expression that captures the trend: minimize some measure of the error Of all the points 6

Interpolation Concentrate first on the case where we believe there is no error in the data (and round-off is assumed to be negligible). So we have yi f(xi) at n 1 points x0,x1 xi, xn: xj xj-1 (Often but not always evenly spaced) In general, we do not know the underlying function f(x) Conceptually, interpolation consists of two stages: – Develop a simple function g(x) that Approximates f(x) Passes through all the points xi – Evaluate f(xt) where x0 xt xn February 6, 2023 OSU/CIS 541 7

Interpolation Clearly, the crucial question is the selection of the simple functions g(x) Types are: – – – – Polynomials Splines Trigonometric functions Spectral functions Rational functions etc February 6, 2023 OSU/CIS 541 8

Curve Approximation We will look at three possible approximations (time permitting): – Polynomial interpolation – Spline (polynomial) interpolation – Least-squares (polynomial) approximation If you know your function is periodic, then trigonometric functions may work better. – Fourier Transform and representations February 6, 2023 OSU/CIS 541 9

Polynomial Interpolation Consider our data set of n 1 points yi f(xi) at n 1 points x0,x1 xi, xn: xj xj-1 In general, given n 1 points, there is a unique polynomial gn(x) of order n: 2 g n ( x) a0 a1 x a2 x an x n That passes through all n 1 points February 6, 2023 OSU/CIS 541 10

Polynomial Interpolation There are a variety of ways of expressing the same polynomial Lagrange interpolating polynomials Newton’s divided difference interpolating polynomials We will look at both forms February 6, 2023 OSU/CIS 541 11

Polynomial Interpolation Existence – does there exist a polynomial that exactly passes through the n data points? Uniqueness – Is there more than one such polynomial? – We will assume uniqueness for now and prove it latter. February 6, 2023 OSU/CIS 541 12

Lagrange Polynomials Summation of terms, such that: n – Equal to f() at a data pn ( x) Li ( x) f ( xi ) point. i 0 – Equal to zero at all n x xk other data points. Li ( x) k 0, k i xi xk – Each term is a nthdegree polynomial 1 i j Existence!!! February 6, 2023 Li ( x j ) ij 0 i j OSU/CIS 541 13

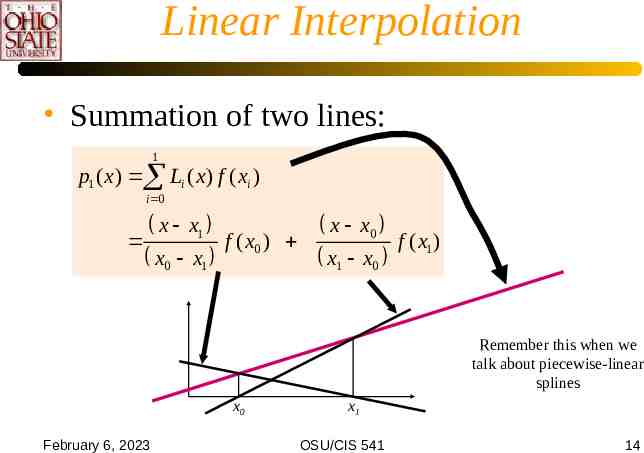
Linear Interpolation Summation of two lines: 1 p1 ( x) Li ( x ) f ( xi ) i 0 x x1 x0 x1 f ( x0 ) x x0 x1 x0 f ( x1 ) Remember this when we talk about piecewise-linear splines x0 February 6, 2023 x1 OSU/CIS 541 14

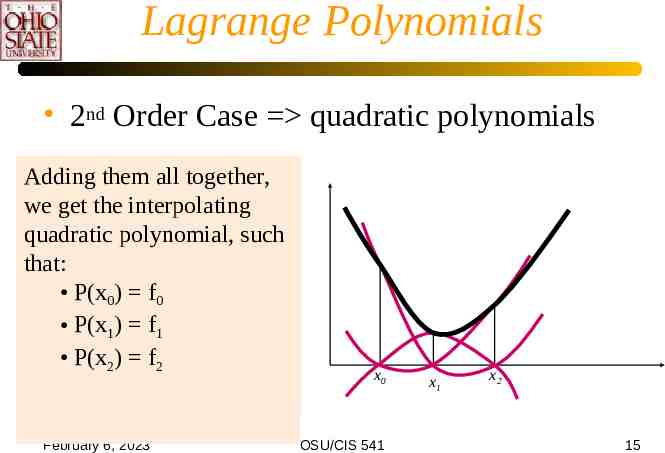
Lagrange Polynomials 2nd Order Case quadratic polynomials The first third quadratic hashas Adding them all together, quadratic has second quadratic we getatthe interpolating roots x10 and x21 and a quadratic polynomial, such value equal to the function that: at x21. data at x0 . P(x P(x00)) f00 P(x P(x011)) f0f011 P(x P(x122)) 0ff21 P(x2) 0 February 6, 2023 x0 OSU/CIS 541 x1 x2 15

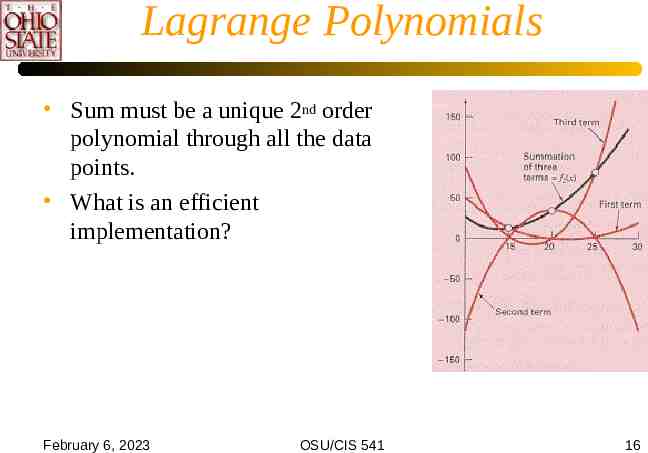
Lagrange Polynomials Sum must be a unique 2nd order polynomial through all the data points. What is an efficient implementation? February 6, 2023 OSU/CIS 541 16

Newton Interpolation Consider our data set of n 1 points yi f(xi) at x0,x1 xi, xn: xn x0 Since pn(x) is the unique polynomial pn(x) of order n, write it: pn ( x) b0 b1 ( x x0 ) b2 ( x x0 )( x x1 ) bn ( x x0 )( x x1 ) ( x x n 1) b0 f ( x0 ) b1 f x1 , x0 f ( x1 ) f ( x0 ) x1 x0 b2 f x2 , x1 , x0 f [ x2 , x1 ] f [ x1 , x0 ] x2 x0 bn f xn , xn 1 , , x0 f xn , , x1 f xn 1 , , x0 xn x0 f[xi,xj] is a first divided difference f[x2,x1,x0] is a second divided difference, etc. February 6, 2023 OSU/CIS 541 17

Invariance Theorem Note, that the order of the data points does not matter. All that is required is that the data points are distinct. Hence, the divided difference f[x0, x1, , xk] is invariant under all permutations of the xi‘s. February 6, 2023 OSU/CIS 541 18

Linear Interpolation Simple linear interpolation results from having only 2 data points. f ( x1 ) f ( x0 ) p1 ( x) f ( x0 ) ( x x0 ) x1 x0 slope x0 February 6, 2023 x1 OSU/CIS 541 19

Quadratic Interpolation Three data points: p2 ( x) f ( x0 ) f ( x1 ) f ( x0 ) ( x x0 ) f [ x0 , x1 , x2 ]( x x0 )( x x1 ) x1 x0 f ( x2 ) f ( x1 ) x x f ( x1 ) f ( x0 ) 2 1 f ( x0 ) ( x x0 ) x1 x0 f ( x0 ) f ( x1 ) f ( x0 ) x1 x0 f ( x1 ) f ( x0 ) x x ( x x )( x x ) 1 0 0 1 x 2 x0 ( x x0 ) f ( x2 ) f ( x1 ) ( x x1 ) ( x x0 ) x x 2 1 x2 February 6, 2023 f ( x1 ) f ( x0 ) ( x x0 ) ( x x1 ) x x 1 0 x0 OSU/CIS 541 20

Newton Interpolation Let’s look at the recursion formula: bn f xn , xn 1 , , x0 f xn , , x1 f xn 1 , , x0 xn x0 where f [ xi ] f ( xi ) For the quadratic term: f ( x2 ) f ( x1 ) f ( x1 ) f ( x0 ) f [ x2 , x1 ] f [ x1 , x0 ] x2 x1 x1 x0 b2 f x2 , x1 , x0 x2 x0 x2 x0 f ( x2 ) f ( x1 ) b1 x2 x1 x2 x0 February 6, 2023 OSU/CIS 541 21

Evaluating for x2 f ( x2 ) b0 b1 x2 x0 b2 x2 x0 x2 x1 f 2 f1 f 0 b1 x2 x0 b1 x2 x1 x2 x1 f 0 b1 x1 x0 f 2 f1 f1 f 0 f0 x1 x0 f 2 f1 x1 x0 f2 February 6, 2023 OSU/CIS 541 22

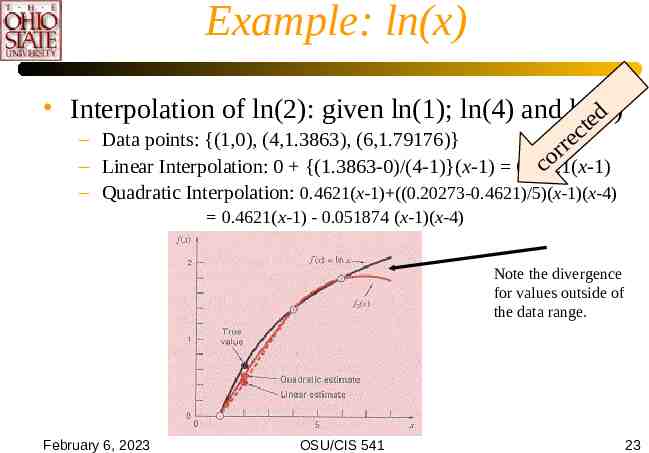
Example: ln(x) Interpolation of ln(2): given ln(1); ln(4) and ln(6) ed t c – Data points: {(1,0), (4,1.3863), (6,1.79176)} e rr o – Linear Interpolation: 0 {(1.3863-0)/(4-1)}(x-1) 0.4621(x-1) c – Quadratic Interpolation: 0.4621(x-1) ((0.20273-0.4621)/5)(x-1)(x-4) 0.4621(x-1) - 0.051874 (x-1)(x-4) Note the divergence for values outside of the data range. February 6, 2023 OSU/CIS 541 23

Example: ln(x) Quadratic interpolation catches some of the curvature Improves the result somewhat Not always a good idea: see later February 6, 2023 OSU/CIS 541 24

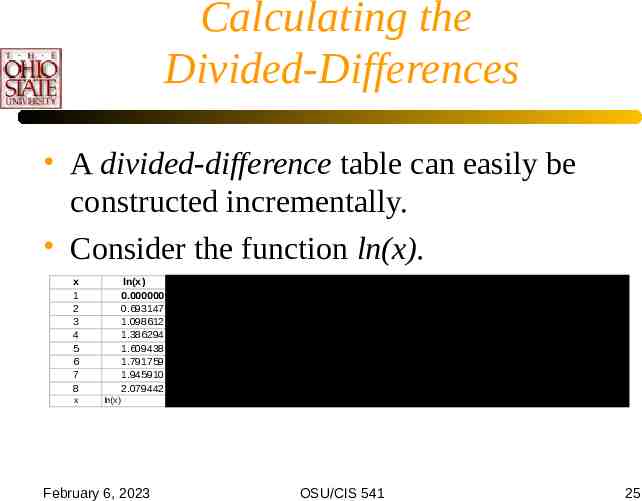
Calculating the Divided-Differences A divided-difference table can easily be constructed incrementally. Consider the function ln(x). x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 25

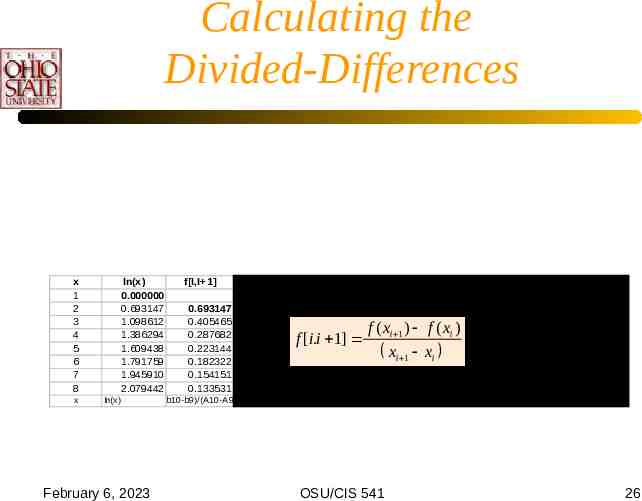
Calculating the Divided-Differences x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 f [i.i0.028317 1] 0.008874 0.003953 0.002109 0.001259 f ( xi 1 ) f ( xi ) -0.004861 xi 1 xi -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 26

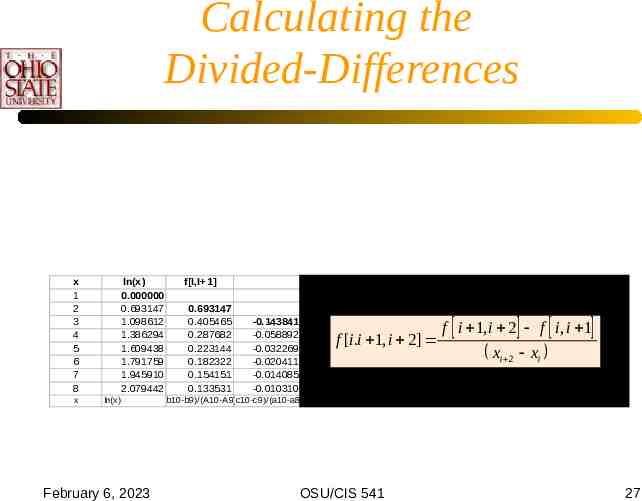
Calculating the Divided-Differences x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 f [i.i 1,-0.004861 i 2] -0.001230 -0.000461 -0.000212 f i 1, i 2 f i, i 1 x xi 0.000726 i 2 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 27

Calculating the Divided-Differences f [i, , i 3] x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f i 1, i 2, i 3 f i, i 1, i 2 xi 3 xi f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 28

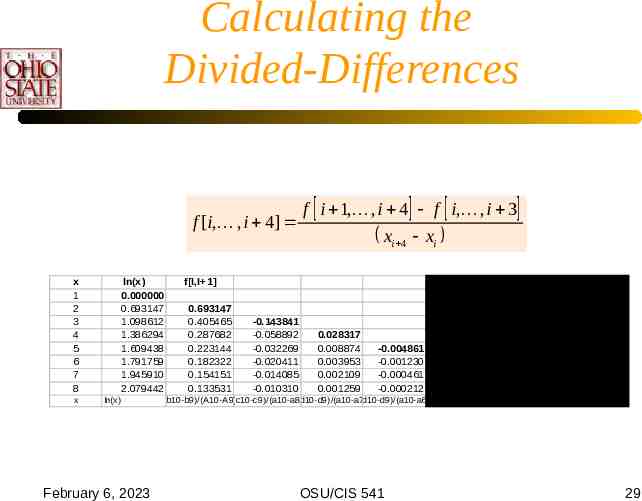
Calculating the Divided-Differences f [i, , i 4] x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f i 1, , i 4 f i, , i 3 xi 4 xi f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 29

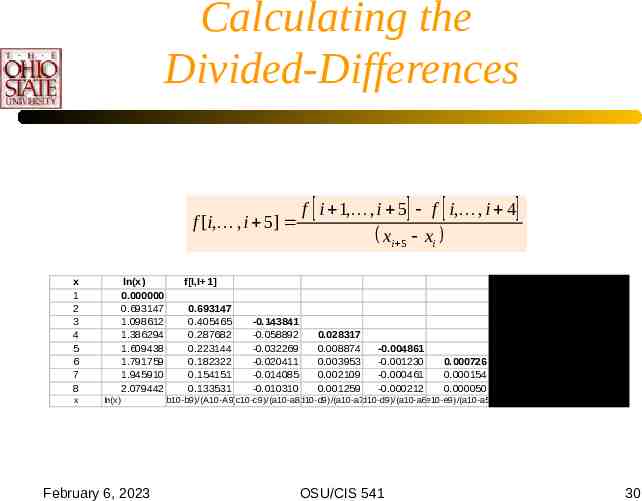
Calculating the Divided-Differences f [i, , i 5] x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f i 1, , i 5 f i, , i 4 xi 5 xi f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 30

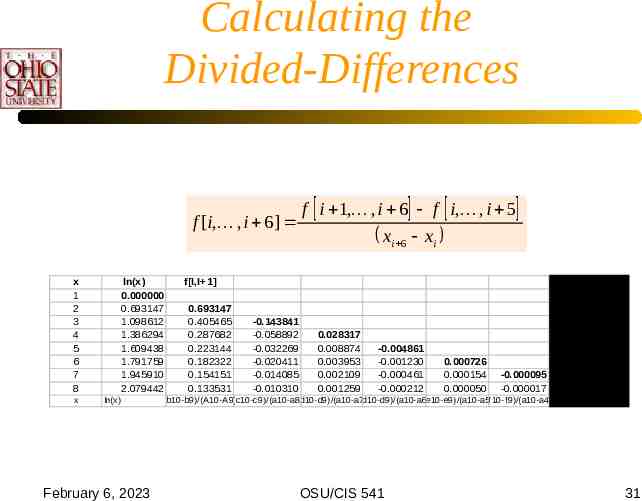
Calculating the Divided-Differences f [i, , i 6] x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f i 1, , i 6 f i, , i 5 xi 6 xi f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000013 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 31

Calculating the Divided-Differences Finally, we can calculate the last coefficient. f [i, , i 7] x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 f i 1, , i 7 f i, , i 6 xi 7 xi f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 f[I,I 1, ,I 7] -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000011 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 32

Calculating the Divided-Differences All of the coefficients for the resulting polynomial are in b0 bold. x 1 2 3 4 5 6 7 8 x ln(x) 0.000000 0.693147 1.098612 1.386294 1.609438 1.791759 1.945910 2.079442 ln(x) February 6, 2023 b4 f[I,I 1] 0.693147 0.405465 0.287682 0.223144 0.182322 0.154151 0.133531 -0.143841 -0.058892 -0.032269 -0.020411 -0.014085 -0.010310 b7 f[I,I 1, ,I 7] 0.028317 0.008874 0.003953 0.002109 0.001259 -0.004861 -0.001230 -0.000461 -0.000212 0.000726 0.000154 0.000050 -0.000095 -0.000017 0.000011 (b10-b9)/(A10-A9) (c10-c9)/(a10-a8) (d10-d9)/(a10-a7) (d10-d9)/(a10-a6) (e10-e9)/(a10-a5) (f10-f9)/(a10-a4) (g10-g9)/(a10-a3) OSU/CIS 541 33

Polynomial Form for DividedDifferences The resulting polynomial comes from the divided-differences and the corresponding product terms: p7 x 0 0.693 x 1 0.144 x 1 x 2 0.28 x 1 x 2 x 3 0.0049 x 1 x 2 x 3 x 4 7.26 10 4 x 1 x 2 x 3 x 4 x 5 9.5 10 5 x 1 x 2 x 3 x 4 x 5 x 6 1.1 10 5 x 1 x 2 x 3 x 4 x 5 x 6 x 7 February 6, 2023 OSU/CIS 541 34

Many polynomials Note, that the order of the numbers (x i,yi)’s only matters when writing the polynomial down. – The first column represents the set of linear splines between two adjacent data points. – The second column gives us quadratics thru three adjacent points. – Etc. February 6, 2023 OSU/CIS 541 35

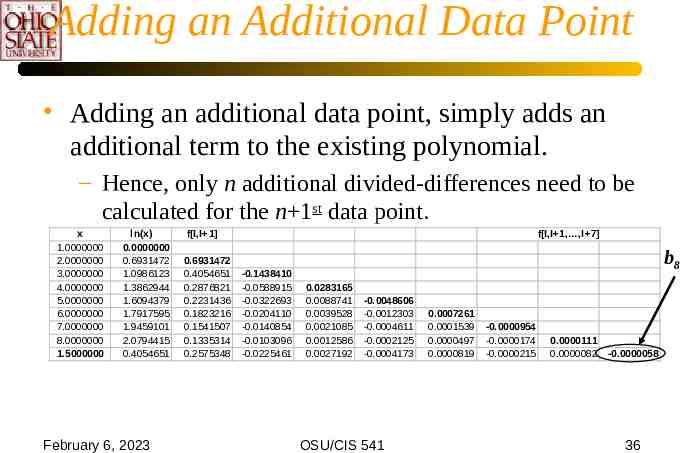
Adding an Additional Data Point Adding an additional data point, simply adds an additional term to the existing polynomial. – Hence, only n additional divided-differences need to be calculated for the n 1st data point. x 1.0000000 2.0000000 3.0000000 4.0000000 5.0000000 6.0000000 7.0000000 8.0000000 1.5000000 ln(x) 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379 1.7917595 1.9459101 2.0794415 0.4054651 February 6, 2023 f[I,I 1] 0.6931472 0.4054651 0.2876821 0.2231436 0.1823216 0.1541507 0.1335314 0.2575348 f[I,I 1, ,I 7] -0.1438410 -0.0588915 -0.0322693 -0.0204110 -0.0140854 -0.0103096 -0.0225461 b8 0.0283165 0.0088741 0.0039528 0.0021085 0.0012586 0.0027192 -0.0048606 -0.0012303 -0.0004611 -0.0002125 -0.0004173 OSU/CIS 541 0.0007261 0.0001539 0.0000497 0.0000819 -0.0000954 -0.0000174 -0.0000215 0.0000111 0.0000082 -0.0000058 36

Adding More Data Points Quadratic interpolation: – does linear interpolation – Then add higher-order correction to catch the curvature Cubic, Consider the case where the data points are organized such the the first two are the endpoints, the next point is the mid-point, followed by successive mid-points of the half-intervals. – Worksheet: f(x) x2 from -1 to 3. February 6, 2023 OSU/CIS 541 37

Uniqueness Suppose that two polynomials of degree n (or less) existed that interpolated to the n 1 data points. Subtracting these two polynomials from each other also leads to a polynomial of at most n degree. rn ( x) pn ( x) qn ( x) February 6, 2023 OSU/CIS 541 38

Uniqueness Since p and q both interpolate the n 1 data points, This polynomial r, has at least n 1 roots!!! This can not be! A polynomial of degree-n can only have at most n roots. n Therefore, r(x) 0 pn ( x) an ( x ri ) i 1 n 1 pn 1 ( x) an 1 ( x ri ) i 1 February 6, 2023 OSU/CIS 541 39

Example Suppose f was a polynomial of degree m, where m n. Ex: f(x) 3x-2 We have evaluations of f(x) at five locations: (-2,-8), (-1,-5), (0,-2), (1,1), (2,4) February 6, 2023 OSU/CIS 541 40

Error Define the error term as: n ( x ) f ( x ) pn ( x ) If f(x) is an nth order polynomial pn(x) is of course exact. Otherwise, since there is a perfect match at x0, x1, ,xn This function has at least n 1 roots at the interpolation points. n ( x) ( x x0 )( x x1 ) ( x xn )h( x) February 6, 2023 OSU/CIS 541 41

Interpolation Errors n 1 ( n 1) n ( x ) f ( x ) pn ( x ) f x xi (n 1)! i 0 x [a, b], a, b Proof is in the book. Intuitively, the first n 1 terms of the Taylor Series is also an nth degree polynomial. February 6, 2023 OSU/CIS 541 42

Interpolation Errors Use the point x, to expand the polynomial. x {x0 , x1 , xn } n n ( x) f ( x) pn ( x) f [ x0 , x1 , xn , x] x xi i 0 Point is, we can take an arbitrary point x, and create an (n 1)th polynomial that goes thru the point x. February 6, 2023 OSU/CIS 541 43

Interpolation Errors Combining the last two statements, we can also get a feel for what these divided differences represent. 1 (n) f [ x0 , x1 , xn ] f n! Corollary 1 in book – If f(x) is a polynomial of degree m n, then all (m 1)st divided differences and higher are zero. February 6, 2023 OSU/CIS 541 44

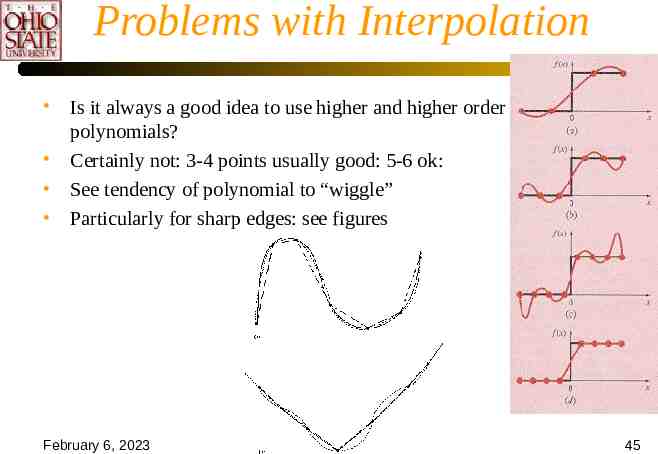
Problems with Interpolation Is it always a good idea to use higher and higher order polynomials? Certainly not: 3-4 points usually good: 5-6 ok: See tendency of polynomial to “wiggle” Particularly for sharp edges: see figures February 6, 2023 OSU/CIS 541 45

Chebyshev nodes Equally distributed points may not be the optimal solution. If you could select the xi’s, what would they be? Want to minimize the x xterm. These are the Chebyshev nodes. n i i 0 – For x -1 to 1: February 6, 2023 i xi cos , (0 i n) n OSU/CIS 541 46

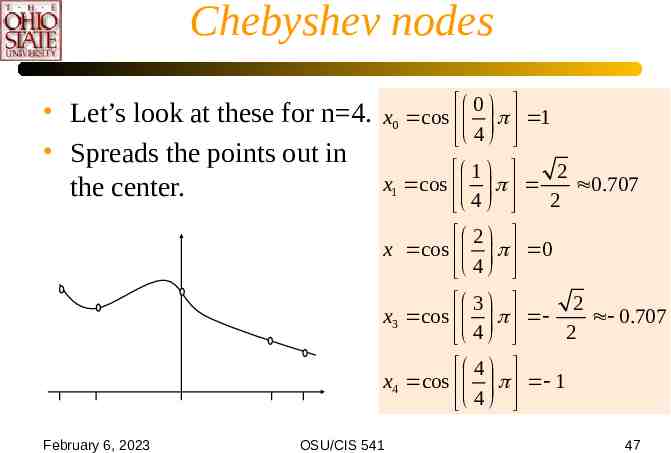
Chebyshev nodes Let’s look at these for n 4. Spreads the points out in the center. 0 x0 cos 1 4 1 2 x1 cos 0.707 2 4 2 x cos 0 4 3 2 x3 cos 0.707 2 4 4 x4 cos 1 4 February 6, 2023 OSU/CIS 541 47

Polynomial Interpolation in Two-Dimensions Consider the case in higher-dimensions. February 6, 2023 OSU/CIS 541 48

Finding the Inverse of a Function What if I am after the inverse of the function f(x)? – For example arccos(x). Simply reverse the role of the xi and the fi. February 6, 2023 OSU/CIS 541 49