Module #21 – Relations University of Florida Dept. of Computer
39 Slides178.50 KB

Module #21 - Relations University of Florida Dept. of Computer & Information Science & Engineering COT 3100 Applications of Discrete Structures Dr. Michael P. Frank Slides for a Course Based on the Text Discrete Mathematics & Its Applications (5th Edition) by Kenneth H. Rosen 02/12/24 (c)2001-2003, Michael P. Frank 1

Module #21 - Relations Module #21: Relations Rosen 5th ed., ch. 7 35 slides (in progress), 2 lectures 02/12/24 (c)2001-2003, Michael P. Frank 2

Module #21 - Relations Binary Relations Let A, B be any sets. A binary relation R from A to B, written (with signature) R:A B, or R:A,B, is (can be identified with) a subset of the set A B. – E.g., let : N N : {(n,m) n m} The notation a R b or aRb means that (a,b) R. – E.g., a b means (a,b) If aRb we may say “a is related to b (by relation R)”, – or just “a relates to b (under relation R)”. A binary relation R corresponds to a predicate function PR:A B {T,F} defined over the 2 sets A,B; – e.g., predicate “eats” : {(a,b) organism a eats food b} 02/12/24 (c)2001-2003, Michael P. Frank 3

Module #21 - Relations Complementary Relations Let R:A,B be any binary relation. Then, R:A B, the complement of R, is the binary relation defined by R : {(a,b) (a,b) R} (A B) R Note this is just R if the universe of discourse is U A B; thus the name complement. Note the complement of R is R. Example: {(a,b) (a,b) } {(a,b) a b} 02/12/24 (c)2001-2003, Michael P. Frank 4

Module #21 - Relations Inverse Relations Any binary relation R:A B has an inverse relation R 1:B A, defined by R 1 : {(b,a) (a,b) R}. E.g., 1 {(b,a) a b} {(b,a) b a} . E.g., if R:People Foods is defined by a R b a eats b, then: b R 1 a b is eaten by a. (Passive voice.) 02/12/24 (c)2001-2003, Michael P. Frank 5

Module #21 - Relations Relations on a Set A (binary) relation from a set A to itself is called a relation on the set A. E.g., the “ ” relation from earlier was defined as a relation on the set N of natural numbers. The (binary) identity relation IA on a set A is the set {(a,a) a A}. 02/12/24 (c)2001-2003, Michael P. Frank 6

Module #21 - Relations Reflexivity A relation R on A is reflexive if a A, aRa. – E.g., the relation : {(a,b) a b} is reflexive. A relation R is irreflexive iff its complementary relation R is reflexive. – Example: is irreflexive, because is reflexive. – Note “irreflexive” does NOT mean “not reflexive”! For example: the relation “likes” between people is not reflexive, but it is not irreflexive either. – Since not everyone likes themselves, but not everyone dislikes themselves either! 02/12/24 (c)2001-2003, Michael P. Frank 7

Module #21 - Relations Symmetry & Antisymmetry A binary relation R on A is symmetric iff R R 1, that is, if (a,b) R (b,a) R. – E.g., (equality) is symmetric. is not. – “is married to” is symmetric, “likes” is not. A binary relation R is antisymmetric if a b, (a,b) R (b,a) R. – Examples: is antisymmetric, “likes” is not. – Exercise: prove this definition of antisymmetric is equivalent to the statement that R R 1 IA. 02/12/24 (c)2001-2003, Michael P. Frank 8

Module #21 - Relations Transitivity A relation R is transitive iff (for all a,b,c) (a,b) R (b,c) R (a,c) R. A relation is intransitive iff it is not transitive. Some examples: – – – 02/12/24 “is an ancestor of” is transitive. “likes” between people is intransitive. “is located within 1 mile of” is ? (c)2001-2003, Michael P. Frank 9

Module #21 - Relations Totality A relation R:A B is total if for every a A, there is at least one b B such that (a,b) R. If R is not total, then it is called strictly partial. A partial relation is a relation that might be strictly partial. (Or, it might be total.) – In other words, all relations are considered “partial.” 02/12/24 (c)2001-2003, Michael P. Frank 10

Module #21 - Relations Functionality A relation R:A B is functional if, for any a A, there is at most 1 b B such that (a,b) R. – “R is functional” a A: b1 b2 B: aRb1 aRb2. – Iff R is functional, then it corresponds to a partial function R:A B where R(a) b aRb; e.g. – E.g., The relation aRb : “a b 0” yields the function (a) b. R is antifunctional if its inverse relation R 1 is functional. – Note: A functional relation (partial function) that is also antifunctional is an invertible partial function. R is a total function R:A B if it is both functional and total, that is, for any a A, there is exactly 1 b such that (a,b) R. I.e., a A: !b: aRb. – If R is functional but not total, then it is a strictly partial function. – Exercise: Show that iff R is functional and antifunctional, and both it and its inverse are total, then it is a bijective function. 02/12/24 (c)2001-2003, Michael P. Frank 11

Module #21 - Relations Lambda Notation The lambda calculus is a formal mathematical language for defining and operating on functions. – It is the mathematical foundation of a number of functional (recursive function-based) programming languages, such as LISP and ML. It is based on lambda notation, in which “λa: f(a)” is a way to denote the function f without ever assigning it a specific symbol. – E.g., (λx. 3x2 2x) is a name for the function f:R R where f(x) 3x2 2x. Lambda notation and the “such that” operator “ ” can also be used to compose an expression for the function that corresponds to any given functional relation. – Let R:A B be any functional relation on A,B. – Then the expression (λa: b aRb) denotes the function f:A B where f(a) b iff aRb. E.g., If I write: f : (λa: b a b 0), this is one way of defining the function f(a) a. 02/12/24 (c)2001-2003, Michael P. Frank 12

Module #21 - Relations Composite Relations Let R:A B, and S:B C. Then the composite S R of R and S is defined as: S R {(a,c) b: aRb bSc} Note that function composition f g is an example. Exer.: Prove that R:A A is transitive iff R R R. The nth power Rn of a relation R on a set A can be defined recursively by: R0 : IA ; Rn 1 : Rn R for all n 0. – Negative powers of R can also be defined if desired, by R n : (R 1)n. 02/12/24 (c)2001-2003, Michael P. Frank 13

Module #21 - Relations §7.2: n-ary Relations An n-ary relation R on sets A1, ,An, written (with signature) R:A1 An or R:A1, ,An, is simply a subset R A1 An. The sets Ai are called the domains of R. The degree of R is n. R is functional in the domain Ai if it contains at most one n-tuple ( , ai , ) for any value ai within domain Ai. 02/12/24 (c)2001-2003, Michael P. Frank 14

Module #21 - Relations Relational Databases A relational database is essentially just an n-ary relation R. A domain Ai is a primary key for the database if the relation R is functional in Ai. A composite key for the database is a set of domains {Ai, Aj, } such that R contains at most 1 n-tuple ( ,ai, ,aj, ) for each composite value (ai, aj, ) Ai Aj 02/12/24 (c)2001-2003, Michael P. Frank 15

Module #21 - Relations Selection Operators Let A be any n-ary domain A A1 An, and let C:A {T,F} be any condition (predicate) on elements (n-tuples) of A. Then, the selection operator sC is the operator that maps any (n-ary) relation R on A to the n-ary relation of all n-tuples from R that satisfy C. – I.e., R A, sC(R) {a R sC(a) T} 02/12/24 (c)2001-2003, Michael P. Frank 16

Module #21 - Relations Selection Operator Example Suppose we have a domain A StudentName Standing SocSecNos Suppose we define a certain condition on A, UpperLevel(name,standing,ssn) : [(standing junior) (standing senior)] Then, sUpperLevel is the selection operator that takes any relation R on A (database of students) and produces a relation consisting of just the upperlevel classes (juniors and seniors). 02/12/24 (c)2001-2003, Michael P. Frank 17

Module #21 - Relations Projection Operators Let A A1 An be any n-ary domain, and let {ik} (i1, ,im) be a sequence of indices all falling in the range 1 to n, – That is, where 1 ik n for all 1 k m. Then the projection operator on n-tuples P{ik } : A Ai1 Aim is defined by: P{ik } (a1 ,., an ) (ai1 ,., aim ) 02/12/24 (c)2001-2003, Michael P. Frank 18

Module #21 - Relations Projection Example Suppose we have a ternary (3-ary) domain Cars Model Year Color. (note n 3). Consider the index sequence {ik} 1,3. (m 2) Then the projection P{i }simply maps each tuple k (a1,a2,a3) (model,year,color) to its image: (ai1 , ai2 ) (a1 , a3 ) (model, color) This operator can be usefully applied to a whole relation R Cars (a database of cars) to obtain a list of the model/color combinations available. 02/12/24 (c)2001-2003, Michael P. Frank 19

Module #21 - Relations Join Operator Puts two relations together to form a sort of combined relation. If the tuple (A,B) appears in R1, and the tuple (B,C) appears in R2, then the tuple (A,B,C) appears in the join J(R1,R2). – A, B, and C here can also be sequences of elements (across multiple fields), not just single elements. 02/12/24 (c)2001-2003, Michael P. Frank 20

Module #21 - Relations Join Example Suppose R1 is a teaching assignment table, relating Professors to Courses. Suppose R2 is a room assignment table relating Courses to Rooms,Times. Then J(R1,R2) is like your class schedule, listing (professor,course,room,time). 02/12/24 (c)2001-2003, Michael P. Frank 21

Module #21 - Relations §7.3: Representing Relations Some ways to represent n-ary relations: – With an explicit list or table of its tuples. – With a function from the domain to {T,F}. Or with an algorithm for computing this function. Some special ways to represent binary relations: – With a zero-one matrix. – With a directed graph. 02/12/24 (c)2001-2003, Michael P. Frank 22

Module #21 - Relations Using Zero-One Matrices To represent a binary relation R:A B by an A B 0-1 matrix MR [mij], let mij 1 iff (ai,bj) R. E.g., Suppose Joe likes Susan and Mary, Fred likes Mary, and Mark likes Sally. Then the 0-1 matrix Susan Mary Sally representation Joe 1 1 0 of the relation 0 Fred 1 0 Likes:Boys Girls relation is: Mark 0 0 1 02/12/24 (c)2001-2003, Michael P. Frank 23

Module #21 - Relations Zero-One Reflexive, Symmetric Terms: Reflexive, non-reflexive, irreflexive, symmetric, asymmetric, and antisymmetric. – These relation characteristics are very easy to recognize by inspection of the zero-one matrix. Symmetric: all identical across diagonal (c)2001-2003, Michael P. Frank 0 1 0 1 0 0 ng 0 hi yt an g 02/12/24 in Reflexive: Irreflexive: all 1’s on diagonal all 0’s on diagonal 1 1 0 th any- 0 thing 0 0 any thing 0 y an any- 1 thing 1 any- 1 thing 1 Antisymmetric: all 1’s are across from 0’s 24

Module #21 - Relations Using Directed Graphs A directed graph or digraph G (VG,EG) is a set VG of vertices (nodes) with a set EG VG VG of edges (arcs,links). Visually represented using dots for nodes, and arrows for edges. Notice that a relation R:A B can be represented as a graph GR (VG A B, EG R). Matrix representation MR: Susan Mary Sally Joe 1 1 0 Fred 0 1 0 Mark 0 0 1 02/12/24 Graph rep. GR: Edge set EG (blue arrows) Joe Fred Mark (c)2001-2003, Michael P. Frank Susan Mary Sally Node set VG (black dots) 25
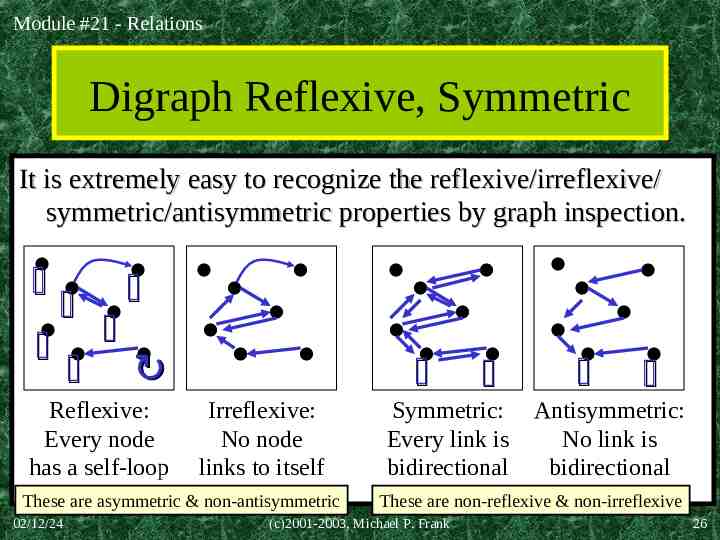
Module #21 - Relations Digraph Reflexive, Symmetric It is extremely easy to recognize the reflexive/irreflexive/ symmetric/antisymmetric properties by graph inspection. Reflexive: Every node has a self-loop Irreflexive: No node links to itself These are asymmetric & non-antisymmetric 02/12/24 Symmetric: Every link is bidirectional Antisymmetric: No link is bidirectional These are non-reflexive & non-irreflexive (c)2001-2003, Michael P. Frank 26

Module #21 - Relations §7.4: Closures of Relations For any property X, the “X closure” of a set A is defined as the “smallest” superset of A that has the given property. The reflexive closure of a relation R on A is obtained by adding (a,a) to R for each a A. I.e., it is R IA The symmetric closure of R is obtained by adding (b,a) to R for each (a,b) in R. I.e., it is R R 1 The transitive closure or connectivity relation of R is obtained by repeatedly adding (a,c) to R for each (a,b), (b,c) in R. – I.e., it is * R R n n Z 02/12/24 (c)2001-2003, Michael P. Frank 27

Module #21 - Relations Paths in Digraphs/Binary Relations A path of length n from node a to b in the directed graph G (or the binary relation R) is a sequence (a,x1), (x1,x2), , (xn 1,b) of n ordered pairs in EG (or R). – An empty sequence of edges is considered a path of length 0 from a to a. – If any path from a to b exists, then we say that a is connected to b. (“You can get there from here.”) A path of length n 1 from a to itself is called a circuit or a cycle. Note that there exists a path of length n from a to b in R if and only if (a,b) Rn. 02/12/24 (c)2001-2003, Michael P. Frank 28

Module #21 - Relations Simple Transitive Closure Alg. A procedure to compute R* with 0-1 matrices. procedure transClosure(MR:rank-n 0-1 mat.) A : B : MR; for i : 2 to n begin A : A MR; B : B A {join} i i {note A represents R , B represents R i end j 1 4 return B {Alg. takes Θ(n ) time} 02/12/24 (c)2001-2003, Michael P. Frank } 29

Module #21 - Relations A Faster Transitive Closure Alg. procedure transClosure(MR:rank-n 0-1 mat.) A : MR; for i : 1 to log2 n begin A : A (A In); {A represents end return A {Alg. takes only Θ(n3 log n) time!} 02/12/24 (c)2001-2003, Michael P. Frank 2i 1 1 i R } j 1 30

Module #21 - Relations Roy-Warshall Algorithm Uses only Θ(n3) operations! Procedure Warshall(MR : rank-n 0-1 matrix) W : MR for k : 1 to n for i : 1 to n for j : 1 to n wij : wij (wik wkj) return W {this represents R*} wij 1 means there is a path from i to j going only through nodes k 02/12/24 (c)2001-2003, Michael P. Frank 31

Module #21 - Relations §7.5: Equivalence Relations An equivalence relation (e.r.) on a set A is simply any binary relation on A that is reflexive, symmetric, and transitive. – E.g., itself is an equivalence relation. – For any function f:A B, the relation “have the same f value”, or f : {(a1,a2) f(a1) f(a2)} is an equivalence relation, e.g., let m “mother of” then m “have the same mother” is an e.r. 02/12/24 (c)2001-2003, Michael P. Frank 32

Module #21 - Relations Equivalence Relation Examples “Strings a and b are the same length.” “Integers a and b have the same absolute value.” “Real numbers a and b have the same fractional part.” (i.e., a b Z) “Integers a and b have the same residue modulo m.” (for a given m 1) 02/12/24 (c)2001-2003, Michael P. Frank 33

Module #21 - Relations Equivalence Classes Let R be any equiv. rel. on a set A. The equivalence class of a, [a]R : { b aRb } (optional subscript R) – It is the set of all elements of A that are “equivalent” to a according to the eq.rel. R. – Each such b (including a itself) is called a representative of [a]R. Since f(a) [a]R is a function of a, any equivalence relation R can be defined using aRb : “a and b have the same f value”, given f. 02/12/24 (c)2001-2003, Michael P. Frank 34

Module #21 - Relations Equivalence Class Examples “Strings a and b are the same length.” – [a] the set of all strings of the same length as a. “Integers a and b have the same absolute value.” – [a] the set {a, a} “Real numbers a and b have the same fractional part (i.e., a b Z).” – [a] the set { , a 2, a 1, a, a 1, a 2, } “Integers a and b have the same residue modulo m.” (for a given m 1) – [a] the set { , a 2m, a m, a, a m, a 2m, } 02/12/24 (c)2001-2003, Michael P. Frank 35

Module #21 - Relations Partitions A partition of a set A is the set of all the equivalence classes {A1, A2, } for some equivalence relation on A. – The Ai’s are all disjoint and their union A. They “partition” the set into pieces. Within each piece, all members of that set are equivalent to each other. 02/12/24 (c)2001-2003, Michael P. Frank 36

Module #21 - Relations §7.6: Partial Orderings A relation R on A is called a partial ordering or partial order iff it is reflexive, antisymmetric, and transitive. – We often use a symbol looking something like (or analogous shapes) for such relations. – Examples: , on real numbers, , on sets. – Another example: the divides relation on Z . Note it is not necessarily the case that either a b or b a. A set A together with a partial order on A is called a partially ordered set or poset and is denoted (A, ). 02/12/24 (c)2001-2003, Michael P. Frank 37

Module #21 - Relations Posets as Noncyclical Digraphs There is a one-to-one correspondence between posets and the reflexive transitive closures of noncyclical digraphs. – Noncyclical: Containing no directed cycles. Example: consider the poset ({0, ,10}, ) – Its minimal digraph: 02/12/24 1 2 3 5 7 4 6 9 10 (c)2001-2003, Michael P. Frank 8 0 38

Module #21 - Relations More to come More slides on partial orderings to be added in the future 02/12/24 (c)2001-2003, Michael P. Frank 39





