Modeling Infectious Disease Processes CAMRA August 10th, 2006
45 Slides2.24 MB

Modeling Infectious Disease Processes CAMRA August 10th, 2006

Why Use Mathematical Models? Modeling perspective Mathematical models reflect the known causal relationships of a given system. act as data integrators. take on the form of a complex hypothesis. Benefits of modeling Provides information on knowledge gaps. Provide insight into the process that can then be empirically tested. Provides direction for further research activities. Provides explicit description of system (mathematical vs. conceptual models)

Milestones of Modeling Studies The importance of simple models stems not from realism or the accuracy of their predictions but rather from the simple and fundamental principles that they set forth. Three fundamental principles inferred from the study of mathematical models. The propensity of predator-prey systems to oscillate (Lotka and Volterra) The tendency of competing species to exclude one another (Gause, MacAurther) The threshold dependence of epidemics on population size (Kermack and McKendrick).

Classification of Model Structures Statistical vs. Mechanistic Classes of mechanistic models Deterministic vs. Stochastic Continuous vs. Discrete Analytical vs. Computational

History of Mathematical Epidemiology Historical Background Prior to 1850 disease causation was attributed to miasmas mid 1800’s germ theory was developed John Snow identifies the cause of cholera transmission. Early Modeling: William Farr develops a method to describe epidemic phenomena. He fits normal curves to epidemic data.

History of Mathematical Epidemiology Germ theory leads to mass action model of transmission The rate of new cases is directly proportional to the current number of cases and susceptibles Ct 1 r . Ct . St Different than posteriori approach to modeling.

Post-germ Theory Approach to a Priori Modeling William Hamer (1906) First to develop the mass action approach to epidemic theory. Beginnings of the development of a firm theoretical framework for investigation of observed patterns. Ronald Ross (1910's) Used models to demonstrate a threshold effect in malaria transmission.

Post-germ Theory Approach to a Priori Modeling Diagram of a simple infection-recovery system, analogous to Ross’s basic model (Fine, 1975b) Distinguishes between dependent and independent happenings h SUSCEPTIBLE INFECTED r

Post-germ Theory Approach to a Priori Modeling Kermack and McKendrick (1927) Mass action. Developed epidemic model taking into consideration susceptible, infected, and immune. Conclusions An epidemic is not necessarily terminated by the exhaustion of the susceptible. There exists a threshold density of population. Epidemic increases as the population density is increased. The greater the initial susceptible density the smaller it will be at the end of the epidemic. The termination of an epidemic may result from a particular relation between the population density, and the infectivity, recovery, and death rates.

Post-germ Theory Approach to a Priori Modeling Major contributors since Kermack and McKendrick Wade Hampton Frost, Lowell Reed (1930's). First description of epidemics using a binomial expression George Macdonald (1950's). Furthers the work of Ross. Develops notion of breakpoint in helminth transmission. Roy Anderson and Robert May (1970 - present). Development of a comprehensive framework for infectious disease transmission.

The Microparasites - Viruses, Bacteria, and Protozoa Basic properties Direct reproduction within hosts Small size, short generation time Recovered hosts are often immune for a period of time (often for life) Duration of infection often short relative to life span of host.

The Macroparasites Parasitic Helminths and Arthropods Basic properties No direct reproduction within definitive host Large size, long generation time Many factors depend on the number of parasites in a given host: egg output, pathogenic effects, immune response, parasite death rate, etc. Rarely distributed in an independently random way.

References Used in Lecture Anderson, R. M., and R. May. 1991. Infectious Diseases of humans: Dynamics and Control. Oxford University Press, New York. Fine, P. E. M. 1975a. Ross's a priori pathometry - a perspective. Proceedings of the Royal Society of Medine 68: 547-551. Fine, P. E. M. 1975b. Superinfection - a problem in formulating a problem. Tropical Diseases Bulletin 72: 475-486. Fine, P. E. M. 1979. John Brownlee and the measurement of infectiousness: an historical study in epidemic theory. Journal of the Royal Statistical Society, A 142: 347-362. Kermack, K. O., and A. G. McKendrick. 1927. Contributions to the mathematical theory of epidemics - I. Proceedings of the Royal Society 115A: 700-721. Kermack, K. O., and A. G. McKendrick. 1932. Contributions to the mathematical theory of epidemics - II. The problem of endemicity. Proceedings of the Royal Society 138A: 55-83. Kermack, K. O., and A. G. McKendrick. 1933. Contributions to the mathematical theory of epidemics - II. Further studies of the problem of endemicity. Proceedings of the Royal Society 141A: 94-122. Ross, R. 1915. Some a priori pathometric equations. British Medical Journal 2818: 546-547.

Disease Transmission Application of the “law of mass action” Originally used to describe chemical reactions Hamer (1906) and Ross (1908) proposed it as a model for disease transmission. The rate of new cases is directly proportional to the current number of cases and susceptibles Ct 1 r . Ct . St Assumptions: All individuals – Have equal susceptibility to a disease. – Have equal capacity to transmit. – Are removed from the population after the transmitting period is over.

Disease Transmission Reed-Frost approach Based on the premise that contact between a given susceptible and one or more cases will produce only one new case. Derivation of model The probability that an individual comes into contact with none of the cases is qCt. The probability that an individual comes into contact with one or more cases is 1 - qCt. C t 1 St ( 1 q Ct )

Disease Transmission Reed-Frost approach Assumptions Infection spreads directly from infected to susceptible individuals. After contact, a susceptible individual will be infectious to others only within the following time period. All individuals have a fixed probability of coming into adequate contact with any other specified individual. The individuals are segregated from others outside the group. These conditions remain constant throughout the epidemic.

Reed-Frost Model Measles fit these assumptions well Long term immunity High infectivity Short infectious period Simulation results 100 initial susceptibles 0.97 probability of no contact 25 Final number of susceptibles Final number of susceptibles 20 15 10 5 0 0.9 0.92 0.94 probabiltiy of no contact 0.96 0.98 20 15 10 5 0 0 50 100 Initial number of susceptibles 150 200

Reed-Frost Model Fitting the model to the data from Aycock. 1934 outbreak in a New England boys’ boarding school. Characteristic of a closed community (uniform susceptibility and homogeneous mixing). Data pooled in 12 day intervals. Explanation of poor fit Error in counting susceptibles. Choice of interval. Variation in contact rate. Lack of homogeneity within the school.

Population Dynamics Defined by change, movement, addition or removal of individuals in time. Four biological processes that determine how the number of individuals change through time Birth Death Immigration Emigration Population processes are assumed independent (basis of most population models).

Modeling Populations Model structure based on ordinary differential equations Types of population dynamics models Exponential growth Logistic growth (density dependence) – Relevance to disease ecology - population regulation of disease agents or vectors – Basis of some demographic models Interspecies competition – For example, Aedes albopictus invasion of Aedes triseriatus habitat. Prey-predator Host-parasite – Microparasites – Macroparasites

The Microparasites - Viruses, Bacteria, and Protozoa Basic properties Direct reproduction within hosts Small size, short generation time Recovered hosts are often immune for a period of time (often for life) Duration of infection often short relative to life span of host.

The Infection Process for Microparasites Similarities in transmission processes How transmission processes differ Parametric differences Lifelong immunity, long incubation period (measles), short term immunity (Typhoid Fever), lifelong immunity, short incubation period (polio), no immunity (gonorrhea) Structural differences Direct vs. sexually transmitted, waterborne vs. vectorborne Factors affecting incidence data Disease related latency, incubation, infectious periods Environment related Population density, hygiene, nutrition, other risk factors.

What Can We Do With These Models? Test theoretical predictions against empirical data. How will changes in demographic or biologic factors affect incidence of disease? What is the most effective vaccination strategy for a particular disease agent and environmental setting? What effect does a large-scale vaccination program have on the average age to infection? What are the critical factors for transmission? Many factors influence a process, few dominate outcomes. Role of a simple model: to provide a precise framework on which to build complexity as quantitative understanding improves – As in experiments, some factors are held constant others are varied.

Model Assumptions Population, N, is constant and large. The size of each class is a continuous variable. Birth and natural deaths occur at equal rates; All newborns are susceptible. Population has a negative exponential age structure (average lifetime 1/ .) The population is homogeneous. Mass action governs transmission. , is the likelihood of close contact per infective per day Transmission occurs from contact. Individuals recover and are removed from the infective class Rate is proportional to the # of infectives. Latent period zero. Removal rate from infective class is . The average period of infectivity is 1/( ).

SIS Model S I dS S I I S dt dI S I I I dt

SIS Model Class of diseases for which infection does not confer immunity (e.g., Gonorrhea) Properties of Gonorrhea Gonococcal infection does not confer protective immunity. Individuals who acquire gonorrhea become infectious within a day or two (short latency). Seasonal oscillations of incidence are small. An infectious man is roughly twice as likely to infect a susceptible woman as when the roles are reversed. Five percent of the men are asymptomatic but account for 60-80% of the transmission. Scale and resolution of model. Stratify on gender, sexual activity, etc. Depends on your question of interest.

SIS Model The endemic solution (m g)/b 1 (b 1, m 0.25, g 0.25) 1 0.9 0.8 S 0.7 0.6 0.5 0.4 0.3 dS I 0 S dt I dI 0 I 0 , S dt 0.2 0 0.5 1 1.5 2 I 2.5 3 3.5 4

SIS Model Analysis Calculation of endemic levels ( ) I Criteria for endemic condition 1 Two equilibrium points Which one is stable depends on the above parametric constraint.

SIR Model b dS S I S dt dI S I I I dt dR I R dt S I R

SIR Model The endemic solution (m g)/b 1 (b 1, m 0.25, g 0.25 1 0.9 0.8 0.7 S 0.6 0.5 0.4 0.3 0.2 dS 0 S dt I dI 0 I 0, S dt 0.1 0 0 0.1 0.2 0.3 0.4 0.5 I 0.6 0.7 0.8 0.9 1

SIR Model Endemic conditions. Interested in long-term dynamics so that birth and death processes are important Calculation of endemic levels I ( 1) Criteria for endemic condition 1

SIR Model Two equilibrium points which one is stable depends on the above parametric constraint. Frequency of reoccurring epidemics depend on: Rate of incoming susceptibles. Rate of transmission. Incubation period. Duration of infectiousness.

Variations of the SIS and SIR Model Disease fatality Disease disappears. Final susceptible fraction is positive. Carriers (asymptomatic) Disease is always endemic. Migration between two communities If contact rate is slightly 1 in one community and 1 in the other. – Migration can cause the disappearance of disease. If contact rate is much 1 in one community and 1 in the other. – Migration can cause the disease to remain endemic. Two dissimilar groups/Vectors Endemicity possible even if contact rate for both groups 1.

Summary Anderson and May provide framework for modeling disease transmission – compartmental models Differential equations govern the ‘rate of change’ in each compartment Properties can be deduced from these equations (endemic conditions, equilibrium points, etc.) Packages like Matlab can be used to obtain solutions for S(t) and I(t).

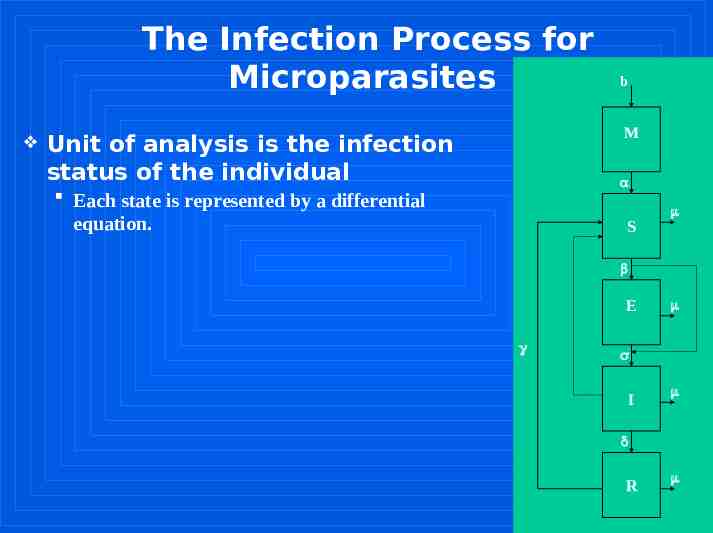
The Infection Process for Microparasites b M Unit of analysis is the infection status of the individual Each state is represented by a differential equation. S E I R

SIS Model Analysis Notation Hethcote uses rather then . Refers to as the contact rate and as the contact number Anderson and May refer to ( /( ) )N as the reproductive rate. Periodic contact rates. Data on incidence rates show a peak between August and October. Model predicts contact rates to peak in summer.

SIR Model Epidemic conditions. Interested in short-term dynamics so that birth and death processes are not important Threshold condition Epidemic features Size of epidemic (peak incidence) Time to peak incidence Number of susceptibles after end of epidemic.

Post-germ Theory Approach to a Priori Modeling Population perspective to infectious disease classification Framework based on population biology rather than taxonomy Two-species prey-predator interaction vs. hostmicroparasite interaction Modeling the viral population dynamics is both not tractable and uninteresting since it misses the one interesting dynamic and that is how the disease is spread.

Analysis of Population Models Studying the behavior of ordinary differential equations Phase plane analysis A portrait of population movement in the N1 - N2 plane. Provides a graphical means to illustrate model properties. Nullclines Sets of points (e.g., a line, curve, or region) that satisfy one of the following equations. Steady state dN 1 dN 2 0 or 0 dt dt (equilibrium points) Points of intersection between the N1 nullcline and the N2 nullcline