Finite Square Well 1
26 Slides749.00 KB
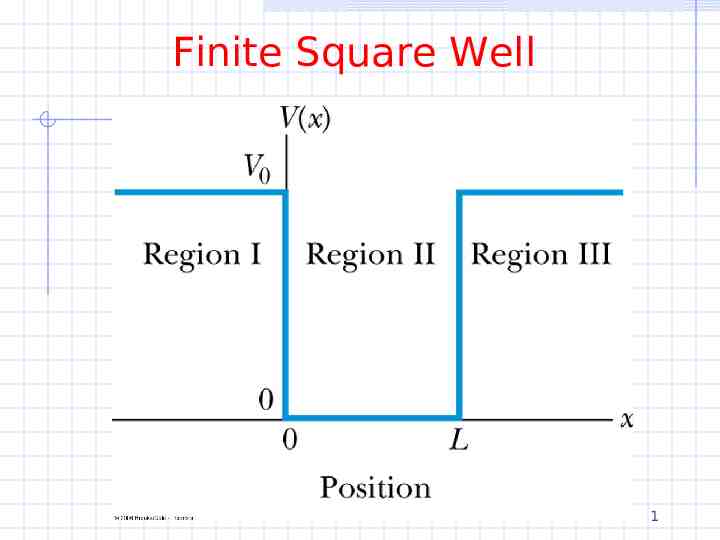
Finite Square Well 1

Finite Square Well In regions I and III 2 d 2 I V I E I 2 2m dx 2m V0 E d 2 I 2 k I I 0 where k I k III dx 2 In region II 2 d 2 II E II 2 2m dx d 2 II 2mE 2 k II II 0 where k II k 2 dx 2

Finite Square Well Solutions in region I and III Ae Ee kI x Be k III x kI x Fe Ae k III x kI x Fe k III x Solutions in region II ikx Ce De ikx or C sin kx D cos kx 3

Finite Square Well The next step is to match boundary conditions inside and out for both ψ and dψ/dx At x 0 A D k I A kC At x L k L Fe I k I Fe C sin kL D cos kL kI L Ck cos kL Dk sin kL 4

Finite Square Well Unfortunately we will not go much further As with the infinite well, application of the boundary conditions leads to energy quantization Although there are 4 equations for 4 unknowns the energy levels must be found numerically or graphically As with the infinite well, the n’th eigenfunction will have n-1 nodes 5
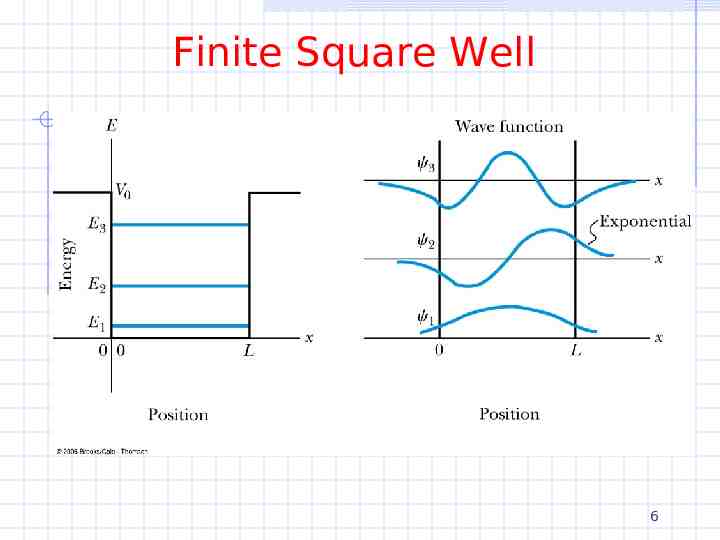
Finite Square Well 6

Harmonic Oscillator The (simple) harmonic oscillator is one of the most important physical systems in physics Any physical system in the neighborhood of a stable equilibrium position can be approximated by a harmonic oscillator (in the limit of small oscillations) Vibrations of atoms in a molecule, oscillations of atoms in a crystal, 7

Harmonic Oscillator Review from classical physics Mass on a spring Fx kx (Hooke' s law) 1 V W Fdx kx 2 2 d 2x k m 2 kx has solution x A cos t where dt m p2 1 2 E T V kx 2m 2 m 2 A2 2 2 1 sin t kA2 cos2 t 2m 2 1 m 2 A2 2 8

Harmonic Oscillator Consider the neighborhood of the minimum of an arbitrary potential Expand V(x) in a Taylor' s series about the minimum at x x0 2 V ( x ) a b x x0 c x x0 . where a V x0 0 dV x x0 0 dx 1 d 2V c 2 x x0 2 dx b then 1 2 V x c x x0 2 9
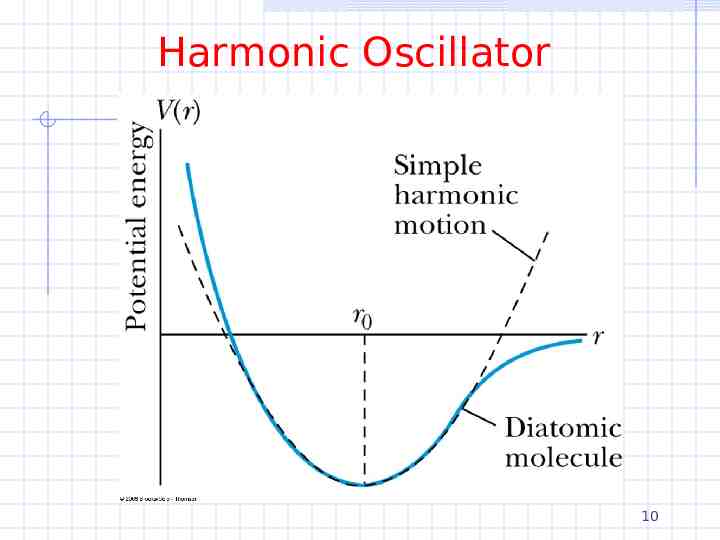
Harmonic Oscillator 10

Harmonic Oscillator We want to solve 2 d 2 1 2 kx E 2 2m dx 2 Unfortunately this is not trivial. And an “easier” method (using ladder operators) is beyond the scope of the class. We will obtain the asymptotic solution however 11

Harmonic Oscillator We start with the time independent Schrodinger equation 2 d 2 1 2 kx E 2 2m dx 2 k 2E m let ω , , y x m d 2 then 2 y 2 0 dy 12

Harmonic Oscillator To find the asymptotic solution, we note that y2 and hence ε can be neglected d 2 2 y 0 2 dy d Multiplying by 2 dy 2 2 d d 2 d y 0 dy dy dy 2 d d 2 2 y 2 y 2 dy dy We can neglect the term on the right side thus 1/ 2 d C y 2 2 dy 13

Harmonic Oscillator Since the asymptotic solution and its derivative must vanish at infinity (why?) it must be that C 0 d y dy The solution at infinity is thus y e y2 2 And that was easy compared to the full solution 14

Harmonic Oscillator The (unnormalized) solution for all y is y2 2 y H n y e where H n y are the Hermite polynomials The first few are H 0 y 1 H1 y 2 y H 2 y 2 4 y 2 15

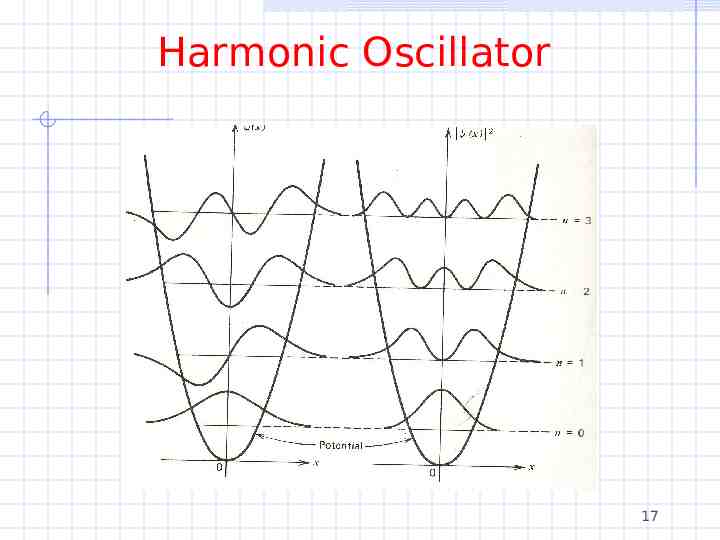
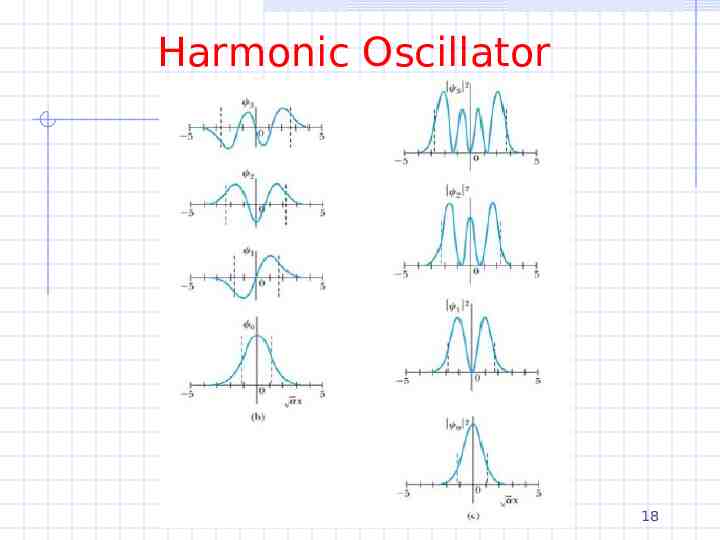
Harmonic Oscillator The normalized wave functions ψ(x) are given in Thornton and Rex (p223) and are not so illuminating You should have be able to sketch the first few wave functions based on your experience with the infinite and finite wells and your knowledge of ψ in general 16
Harmonic Oscillator 17
Harmonic Oscillator 18
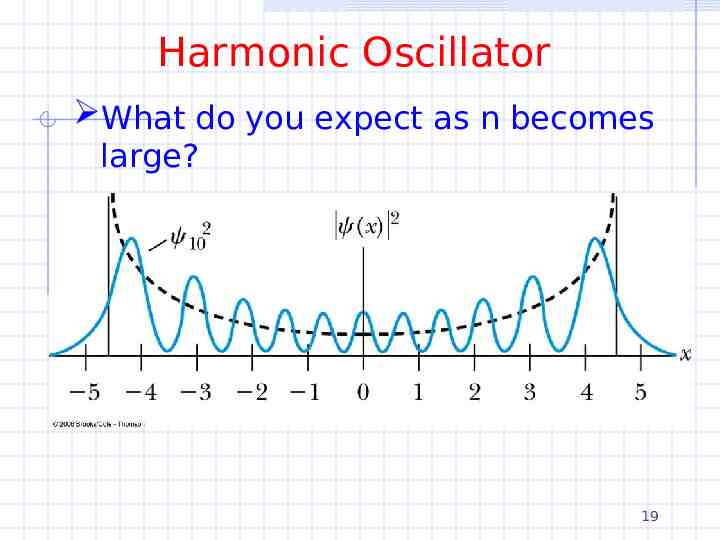
Harmonic Oscillator What do you expect as n becomes large? 19

Harmonic Oscillator In solving the harmonic oscillator problem for all y, the requirement that the wave function vanish at infinity leads to quantized energy The energy levels of the harmonic oscillator are 1 E n with n 0,1,2,. 2 The zero point energy is E0 hω/2 The energy levels are equally spaced This is similar to the Planck relation for radiation Recall we said that standing EM waves in the blackbody cavity arose from harmonic oscillators in the walls 20

Harmonic Oscillator Problem Use the Heisenberg uncertainty principle to estimate the ground state energy of the harmonic oscillator 21

Harmonic Oscillator Problem Let ψ(x,0) A{ψ0(x) ψ1(x)} for the harmonic oscillator Normalize ψ Find ψ(x,t) 2 22

Harmonic Oscillator Problem Consider a potential that has V(x) for x 0 V(x) 1/2kx2 for x 0 What are the possible energy levels? 23

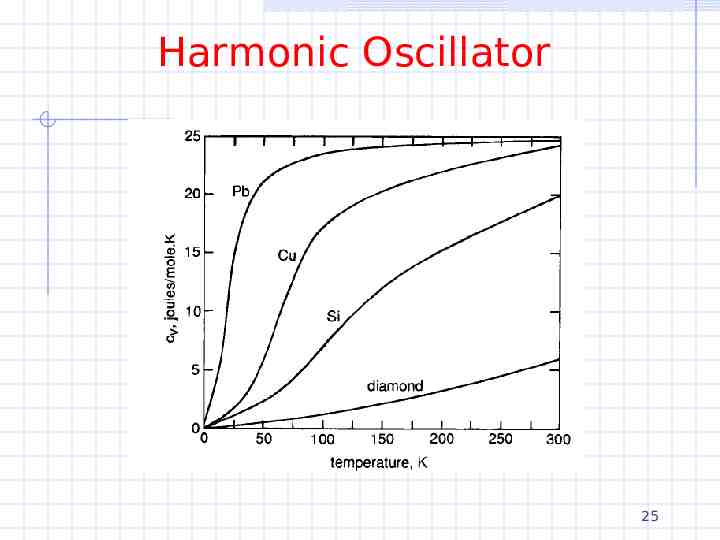
Harmonic Oscillator Einstein used the quantum solution of the harmonic oscillator to solve the temperature dependence of the specific heats of solids Classically f f E Nk BT nRT 2 2 1 dE f CV R n dT 2 For solids CV 3R 25 J/molK This is called the DuLong - Petit law 24
Harmonic Oscillator 25

Harmonic Oscillator If atoms are modeled by quantum harmonic oscillators, explain why specific heats drop as T 0 26