Geometria Analítica Prof. Paulo Salgado [email protected] 1
16 Slides96.56 KB

Geometria Analítica Prof. Paulo Salgado [email protected] 1

Sumário O plano – Produto escalar – Ângulo entre vetores 2

O Plano Produto Escalar e Ângulo entre Vetores O produto escalar entre dois vetores u (x1, y1) e v (x2, y2) é definido como o número: u.v x1.x2 y1.y2 u escalar v Ex: u (2, 1) e v (3, -5) u.v 2.3 1.(-5) 1 3

O Plano Produto Escalar Sendo u, v e w são vetores e k é um número real Propriedades: u.u u 2, se u (x1, y1) verifique a propriedade u.v v.u u.(v w) u.v u.w (k.u).v u.(k.v) k.(u.v) 4

O Plano Produto Escalar Demonstre a propriedade (4) – (k.u).v u.(k.v) k.(u.v) – Demonstração para u (x1, y1) e v (x2, y2) – De acordo com a definição de produto escalar temos: (k.u).v (kx1)x2 (ky1)y2 u.(kv) x1(kx2) y1(ky2) k(u.v) k(x1.x2 y1.y2) – Como (kx1)x2 (ky1)y2 x1(kx2) y1(ky2) k(x1.x2 y1.y2) – Segue que (k.u).v u.(k.v) k.(u.v) 5

O Plano Produto Escalar Proposição: Sejam u e v vetores arbitrários. Então: u.v u . v Conhecida como Desigualdade de Cauchy-Schwarz 6
O Plano Produto Escalar Existe um único ângulo, medido em radianos, entre 0 e π tal que: cos θ u.v u.v u . v .cos θ u . v – Em algumas aplicações é mais conveniente utilizar esta fórmula Esse ângulo, por definição, é o ângulo entre os vetores u e v Exemplo 1: Se u (0, 2) e v (3, 3), o ângulo entre esses vetores é: cos θ 0.3 2.3 2 θ π radianos 2 4 (0 22). (32 32) 7
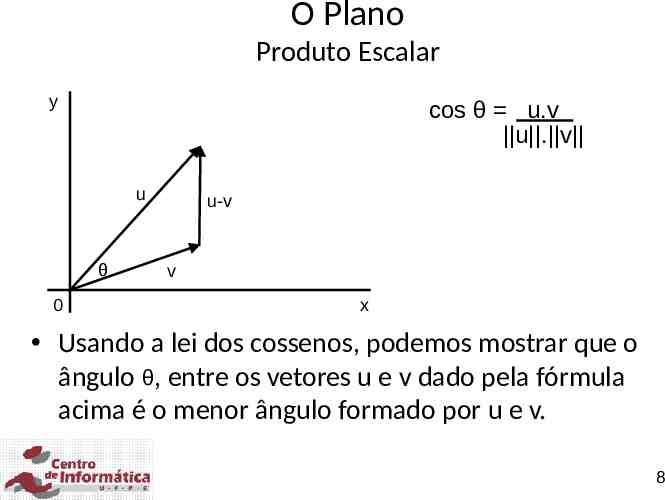
O Plano Produto Escalar y cos θ u.v u . v u θ 0 u-v v x Usando a lei dos cossenos, podemos mostrar que o ângulo θ, entre os vetores u e v dado pela fórmula acima é o menor ângulo formado por u e v. 8

O Plano Produto Escalar Aplicando a lei dos cossenos do triângulo cujos lados são as setas que representam u, v e u-v – Temos: u – v 2 u 2 v 2 - 2 u v cos θ, – de onde temos: cos θ u 2 v 2 - u - v 2 2 u . v – Mas como u 2 v 2 - u - v 2 2u.v (Prove), – Temos cos θ u.v u . v – Se as retas perpendiculares, θ é igual a π/2 radianos, então u . v forem cos π/2 0 u . v 9

O Plano Produto Escalar Se u.v/ u v 0 implica que u.v 0. – Logo, se u e v (onde u 0 e v 0) são perpendiculares, então u.v 0 – u é perpendicular a v u.v 0 10

O Plano Produto Escalar Exemplo 2 (2.31): Sejam u (2, 4) e v (-3, 5). Determine: a) O produto escalar de u por v; b) O ângulo entre u e v; Solução a) u.v (2, 4).(-3, 5) 2.(-3) 4.5 -6 20 14 b) cos θ u.v 14/( 22 42. (-3)2 52) 14/(2 5. 34) u . v cos θ 14/2 170 7/ 170 7 170/170 11

O Plano Produto Escalar Exemplo 3 (2.32): Dado o vetor u (x, y), mostre que os vetores v (y, x) e w (y, -x) são perpendiculares a u e que u v w b) Faça numa figura a representação dos vetores u, v e w Solução v.u (-y, x).(x, y) -xy xy 0 w.u (y, -x).(x, y) yx - xy 0 u v w x2 y2 (-y)2 x2 y2 (-x)2 x2 y2 x2 y2 x2 y2 v (y,-x) -y y 0 -x u (x,y) x w (-y,x) 12

O Plano Produto Escalar Exemplo 4 (2.33): – a) Encontre um vetor de módulo 5 perpendicular ao vetor (2, -1) – b) Determine o valor de x para que o vetor (2, x2 - 1) seja perpendicular ao vetor (-6, 4) Solução v 5 x2 y2 5 x2 y2 25 u.v 0 (2, -1).(x, y) 0 2x – y 0 Logo, x 5 e y 2 5 ou x - 5 e y -2 5 (a) Para (b) x ? para v (2, x2 - 1) e u (-6, 4) Se u.v 0, então (-6, 4). (2, x2 - 1) 0 -12 4x2 – 4 0 4x2 16 x 2 ou x -2 (b) 13

O Plano Produto Escalar Exemplo 5 (2.40): Escreva o vetor (7, -1) como soma de dois vetores, um dos quais é paralelo e o outro é perpendicular ao vetor (1, -1) Solução v u w, onde u é paralelo a (1, -1) e w é perpendicular a (1, -1) u k1(1, -1) w pode ser k2(1, 1) ou k2(-1, -1) como pode ser visto na figura Logo, para o caso 1: (7, -1) u w k1(1, -1) k2(1, 1) (7, -1) (k1, -k1) (k2, k2) k1 k2 7 -k1 k2 -1 k1 4 e k2 3 Para o caso 2: k2(-1,-1) (7, -1) u w k1(1, -1) k2(-1, -1) (7, -1) (k1, -k1) (-k2, -k2) k1 - k2 7 -k1 - k2 -1 k1 4 e k2 -3 Então, para qualquer caso a solução será (7, -1) k1(1, -1) k2(1, 1) k1(1, -1) k2(-1, -1) (4, -4) (3, 3) k2(1,1) (1,-1) 14

O Plano Produto Escalar Exemplo 6 (2.41): Sejam u e v vetores unitários e perpendiculares, w a1u b1v e z a2u b2v. Calcule: (a) w e z , (b) w.z e (c) o ângulo entre w e z Solução u 1, v 1 e u.v 0 (a) w 2 w.w (a1u b1v).(a1u b1v) a1u.a1u a1u.b1v b1v.a1u b1v.b1v, como u e v são perpendicular u.v 0 a1.a1u.u b1.b1v.v a12 u 2 b12 v 2 w a12 u 2 b12 v 2 w a12 b12 e similarmente z a22 b22 (b) w.z (a1u b1v).(a2u b2v) a1u.a2u a1u.b2v b1v. a2u b1v.b2v w.z a1.a2 u 2 0 0 b1.b2 v 2 a1.a2 b1.b2 (c) cos θ w.z/ w . z a1.a2 b1.b2/ a12 b12. a22 b22 θ arccos a1.a2 b1.b2/ a12 b12. a22 b22 15

Hoje vimos. O plano – Produto escalar – Ângulo entre vetores 16






