SERIES DE TIEMPO CON VARIANZA INESTABLE Y CONTAMINADAS
18 Slides1,002.00 KB

SERIES DE TIEMPO CON VARIANZA INESTABLE Y CONTAMINADAS POR OBSERVACIONES ATÍPICAS: UNA ESTIMACIÓN ROBUSTA DE LA TRANSFORMACIÓN DE BOX-COX Elkin Castaño V. Escuela de Estadística, Facultad de Ciencias Universidad Nacional de Colombia, Sede Medellín

Contenido 1. 2. 3. 4. Introducción La Metodología propuesta Experimentos Monte Carlo Conclusiones

1. Introducción En el contexto del análisis de varianza y de regresión, frecuentemente se requiere transformar la variable dependiente para obtener un modelo estructuralmente simple, de forma tal que el término de error que satisfaga: Aditividad, Varianza constante, Normalmente distribuido. Para lograr estos objetivos, Box y Cox (1964), propusieron una transformación de potencia sobre la variable respuesta de forma tal que yi( ) 0 1 xi1 . p xip i En el análisis de series de tiempo, donde los datos son dependientes, Box y Jenkins proponen extender la transformación con el objetivo de estabilizar la varianza de la serie y aproximar la normalidad.

Introducción El procedimiento requiere el conocimiento del proceso ARIMA(p, d, q) que originó la serie de tiempo, cuya especificación general satisface la ecuación ( B)(1 B) d Z t( ) 0 ( B)at , (1) donde d es el orden de integración de la serie, los polinomios ( B) y ( B ) tienen sus ceros fuera del círculo unidad y no tienen factores comunes, 0 es una constante y at es un proceso de ruido blanco de media cero y varianza a2 . es el parámetro de potencia que estabiliza la varianza de Z t , donde Z t( ) Z t 1 si ln( Z ) si t 0 0

Introducción Dado d y bajo el supuesto de normalidad, Box y Jenkins proponen obtener conjuntamente los estimadores de y de los demás parámetros del modelo por medio de la estimación de máxima verosimilitud del modelo ARMA(p, q) asociado a la serie (1 B) d Z t . Para una serie de tiempo estacionaria Z t( ) de longitud n, que sigue un modelo ARMA(p, q), se trata de maximizar con 2 respecto a , 0 , , y a la función de verosimilitud n L( , 0 , , , a2 ) ( n / 2)log(2 ) ( n / 2)log( a2 ) ( ) ( ) 2 ( Z t t ) t 1 2 a2 n ( 1) log( Z t ) , t 1 donde t( ) 1Z t( 1) 2 Zt( 2) . p Zt( p) 1at 1 2 at 2 . q at q . Aunque en muchas ocasiones los investigadores ignoran la inestabilidad de la varianza de la serie, es importante señalar que estas series no pertenecen a la clase de modelos ARIMA.

Introducción Ejemplo 1. Una serie estacionaria en nivel con varianza inestable. Simulación de una serie de tiempo Z t( ) con 0.5 generada por Modelo ARMA(1,0). Serie Zt (no estacionaria) Serie Z t0.5 (estacionaria) Z t no es estable en varianza, no pertenece a la clase ARMA. Z t0.5 es estacionaria.
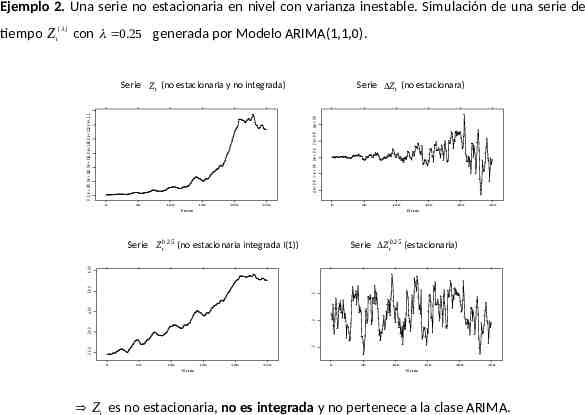
Ejemplo 2. Una serie no estacionaria en nivel con varianza inestable. Simulación de una serie de tiempo Z t( ) con 0.25 generada por Modelo ARIMA(1,1,0). Serie Z t (no estacionara) -4 e 0 9 -2 e 0 9 0 e 0 0 2 e 0 9 4 e 0 9 0 . 0 e 0 20 . 0 e 1 40 . 0 e 1 60 . 0 e 1 80 . 0 e 1 10 . 0 e 1 1 Serie Z t (no estacionaria y no integrada) 0 50 100 150 200 250 0 50 100 Time 150 200 250 Time Serie Z t0.25 (estacionaria) 200 -5 300 0 400 5 500 600 Serie Z t0.25 (no estacionaria integrada I(1)) 0 50 100 150 Time 200 250 0 50 100 150 200 250 Time Z t es no estacionaria, no es integrada y no pertenece a la clase ARIMA.

Introducción La modelación adecuada de las series anteriores, requiere de la estimación del parámetro . Sin embargo, puesto que la serie observada está afectada por , el procedimiento sugerido por Box y Jenkins para estimar conjuntamente a y los demás parámetros del modelo, presenta dificultades: EL modelo ARIMA(p, d, q) para la serie Z t( ) es desconocido y no es posible identificarlo, pues se desconoce el valor de . La identificación del modelo usando directamente la serie Z t por medio de las técnicas tradicionales puede verse afectada. El modelo puede cambiar con el parámetro de transformación . Granger y Newbold (1986), Gurieroux y Jasiak (2002), Guerrero y Perera (2004) señalan que las autocorrelaciones cambian con el parámetro , y por tanto, fijar la forma elegida para el modelo antes de seleccionar la transformación, puede ser incorrecta.

Introducción Se han presentado soluciones: 1. Varios autores sugieren usar la transformación directamente sobre la serie sin tener en cuenta el modelo. (Transformación incondicional o modelo-independiente). 2. Usar un modelo AR(p*) con p* lo suficientemente grande de forma tal que aproxime adecuadamente el modelo ARMA(p,q) para cualquier , y regresar a la propuesta de Box y Jenkins. (Transformación condicional o modelodependiente). Otro problema frecuente en la determinación del parámetro de transformación, es la existencia de observaciones atípicas en series de tiempo de varianza inestable. Andrews (1971) , Atkinson(1985) señalan que, bajo normalidad, el método de la máxima verosimilitud es sensible a este problema, y por tanto la transformación de Box-Cox no es robusta. Chan (1985), muestra que los distintos tipos de observaciones atípicas pueden tener efectos cualitativamente diferentes. Sus resultados indican que en muestras grandes la ACF muestral puede resultar seriamente afectada ante la existencia de observaciones atípicas AO, LS o TC En particular, una observación atípica aditiva (AO) grande puede anular completamente la información de la ACF muestral.

En el contexto del análisis de regresión, algunos autores tales como Carroll (1980, 1982b), Bickel and Doksum (1981), Powell (1991), Chamberlain (1994), Buchinsky (1995), Marazzi y Yohai (2004), Fitzenberger, Wilke y Zhang (2005), Cheng (2005) proponen estimadores robustos para el parámetro de transformación, reemplazando la verosimilitud normal con una función objetivo que es menos sensible a observaciones atípicas. Foudjo (2013) propone un estimador usando una robustificación del estadístico de Shapiro-Wilk y lo aplica en el contexto de series de tiempo. Castaño (2011) en el marco del análisis de regresión, propone un procedimiento de estimación robusto y no paramétrico del parámetro de la transformación Box-Cox, el cual parece funcionar bien en presencia de observaciones atípicas. Este procedimiento fue empleado por Calle (2015) para obtener la transformación Box-Cox en series estacionarias ARMA con varianza inestable. En esta charla se presentarán los resultados obtenidos en la estimación del parámetro para series ARMA y ARIMA de varianza inestable y en presencia de observaciones atípicas, y su comparación con la transformación tradicional.

Introducción Concretamente, se trata de responder a las preguntas: i) Cuando la serie es gaussiana y estacionaria y no está contaminada por observaciones atípicas: Es indiferente usar el estimador modelo-independiente o el modelo-dependiente bajo máxima verosimilitud? Es decir, funciona bien la aproximación? ii) Cuando la serie es gaussiana y estacionaria y está contaminada por observaciones atípicas: Cómo se afecta el estimador modelo-independiente y el modelo-dependiente bajo máxima verosimilitud? Cómo se comporta el estimador modelo-independiente y el modelo-dependiente bajo el método robusto propuesto? iii) Cuando la serie es gaussiana no estacionaria e integrada y no está contaminada por observaciones atípicas: Es indiferente usar el estimador modelo-independiente y el modelo-dependiente?

2. Metodología propuesta El procedimiento que se propone trata de obtener un estimador del parámetro de transformación en la familia de transformaciones de potencia de Box y Cox, de forma tal que en el modelo de series de tiempo ARIMA(p, d, q) ( B )(1- B) d Z t( ) 0 ( B)at la varianza de Z t( ) sea estable y at sea un proceso de ruido blanco con distribución simétrica (no necesariamente Normal). Para obtener a ̂ , se proponen dos procedimientos. a) Estimador condicional de (modelo-dependiente): Como en general no es posible contar con el modelo ARMA(p, q) que genera a la serie Wt (1 B ) d Zt( ) , algunos autores proponen emplear una aproximación AR(p*) con p* lo suficientemente alto de forma tal que aproxime adecuadamente la estructura de dependencia desconocida. Es decir, si ( B ) tiene todos sus ceros fuera del círculo unidad, se considera el modelo aproximado * ( B)(1 B) d Z t( ) 0 at donde * ( B) 1 ( B) ( B) . (1)

Metodología propuesta Dado p*, el procedimiento de búsqueda del estimador de consta de las siguientes etapas: i) Defina un conjunto de valores para . Generalmente el valor de se encuentra en el intervalo [-2, 2]. Para cada valor de , estime el modelo (1) usando regresión robusta LAD (Least Absolute Deviation) y calcule los residuales de la regresión, ât ( ). Por ejemplo, si d 1, el modelo a estimar será: Z t( ) 0 1* Z t( 1) 2* Z t( 2) . p** Z t( p)* at , donde 1 B es el operador diferencia. Los estimadores para 0 , 1 , 2 ,., p* y a son obtenidos * n minimizado t 1 * * 2 at . ii) Obtenga los residuales normalizados como âtn ( ) ât ( ) , MAD( aˆ t ( )) donde MAD( aˆ t ( )) Mediana{ ât ( ) Mediana{ ât ( )} }. Esta transformación elimina las diferentes escalas de medida en la función objetivo, introducidas al ir cambiando .

Metodología propuesta iii) Calcule los percentiles muestrales p ( ) y 1 p ( ) de âtn ( ) para varios valores de p, 0 p 1. Obtenga 0 .5 ( ) p ( ) 1 p ( ) 2 y defina la función SA( ) 0.5 ( ) p p ( ) 1 p ( ) 2 Bajo el supuesto de que la transformación simetriza la distribución de las innovaciones en el modelo, 0.5 ( ) Por tanto, el valor p ( ) 1 p ( ) ̂ que minimiza 2 a 0 para todo p, 0 p 1. SA( ) es la transformación de potencia en la familia de transformaciones de Box-Cox que simetriza la distribución de las innovaciones.

Metodología propuesta b) Estimador incondicional de (modelo-independiente): Se encuentra el estimador ̂ sin tener en cuenta el modelo ARIMA que genera a Z t( ) . El procedimiento es similar al anterior, pero el modelo considerado es un modelo de mediana, Z t( ) 0 at donde 0 es la mediana de Z t( ) . Alternativamente, se usan las etapas ii) y iii) directamente sobre la serie Z t( ) . Para el caso de una muestra aleatoria, Castaño (1995) muestra ̂ consistente de ̂ . es un estimador

3. Experimentos Monte Carlo Para estimar el parámetro se emplearon: 1. La transformación tradicional de Box-Cox incondicional (modelo-independiente), denotada por BC en los resultados. 2. La transformación tradicional de Box-Cox condicional (modelo-dependiente), usando el modelo aproximado, denotada por BCcond en los resultados. 3. La transformación tradicional de Box-Cox condicional (modelo-dependiente), usando el modelo verdadero modelo, denotada por BCcondv en los resultados. 4. La transformación Box-Cox robusta incondicional (modelo-independiente), usado los percentiles con probabilidades p1 1/16, p2 1/8, p3 1/4, p4 1/2, 1-p3, 1-p2, 1-p1. Se denota como Rob3 en los resultados. 5. La transformación Box-Cox robusta condicional (modelo-dependiente), usando el modelo aproximado bajo estimación LAD y los mismos percentiles de 4. Es denotada por Rob3c en los resultados. 6. La transformación Box-Cox robusta condicional (modelo-dependiente), usando el verdadero modelo bajo estimación LAD, y los mismos percentiles de 4. Es denotada por Rob3cv en los resultados.

Experimentos Monte Carlo Se realizaron 2000 simulaciones para cada modelo considerado usando n 50, 100, 250, 1000. Para el caso no estacionario se emplearon adicionalmente series de longitud 2000, 4000, 10000, 20000, 30000 y 50000. Las simulaciones fueron realizadas en el paquete R y las librerías quantreg, forecast, rugarch y car. Para obtener el modelo AR(p*) aproximado, se empleó la función auto.arima de la librería forecast. Modelos considerados Caso estacionario: Valores de 1, 0.5 1. AR(1) con 0.7 , constante 0 5 , sin observaciones atípicas, at un proceso de ruido blanco Normal de media cero y varianza 4. Zt( ) 0 Zt( 1) at 2. MA(1) con 0.7 , media 5 , sin observaciones atípicas, at un proceso de ruido blanco Normal de media cero y varianza 4. Z t( ) at at 1

Experimentos Monte Carlo AR(1) con 0.7 , con una observación atípica AO, a un proceso de ruido blanco t Normal de media cero y varianza 4. El efecto de la observación atípica se analiza en 3 casos según su magnitud, la cual está dada por media( Zt ) kDesvEstand( Zt ), con k 5, 10 y 15. Z t( ) 0 Dt 1 at (1 B) Caso no estacionario: Valores de 1, 0.5 ARIMA(1, 1, 0) con 0.7 , sin observaciones atípicas, at un proceso de RB Normal de media cero y varianza 4. Z t( ) 0 (1 ) Z t( 1) Z t( 2) at ARIMA(0, 1, 1) con 0.7 , sin observaciones atípicas, a un proceso de RB Normal de t media cero y varianza 4. Z t( ) 0 Z t( 1) at at 1






