Online Cryptography Course Dan Boneh Introduction Course Overview
50 Slides3.04 MB

Online Cryptography Course Dan Boneh Introduction Course Overview Dan Boneh

Welcome Course objectives: Learn how crypto primitives work Learn how to use them correctly and reason about security My recommendations: Take notes Pause video frequently to think about the material Answer the in-video questions Dan Boneh

Cryptography is everywhere Secure communication: – web traffic: HTTPS – wireless traffic: 802.11i WPA2 (and WEP), GSM, Bluetooth Encrypting files on disk: EFS, TrueCrypt Content protection (e.g. DVD, Blu-ray): CSS, AACS User authentication and much much more Dan Boneh
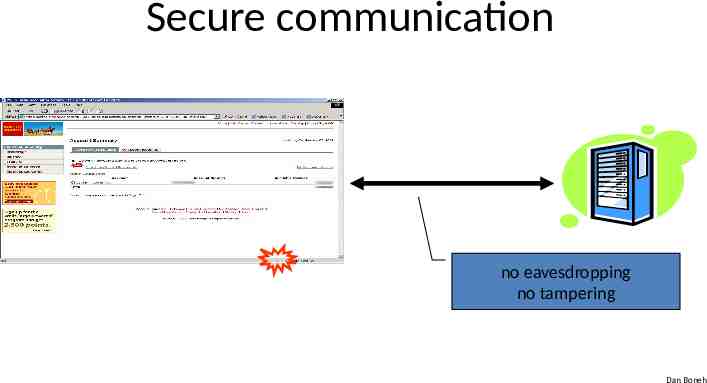
Secure communication no eavesdropping no tampering Dan Boneh

Secure Sockets Layer / TLS Two main parts 1. Handshake Protocol: Establish shared secret key using public-key cryptography (2nd part of course) 2. Record Layer: Transmit data using shared secret key Ensure confidentiality and integrity (1st part of course) Dan Boneh
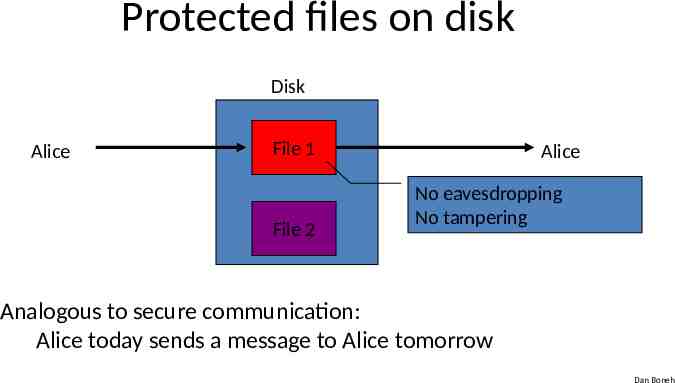
Protected files on disk Disk Alice File 1 File 2 Alice No eavesdropping No tampering Analogous to secure communication: Alice today sends a message to Alice tomorrow Dan Boneh
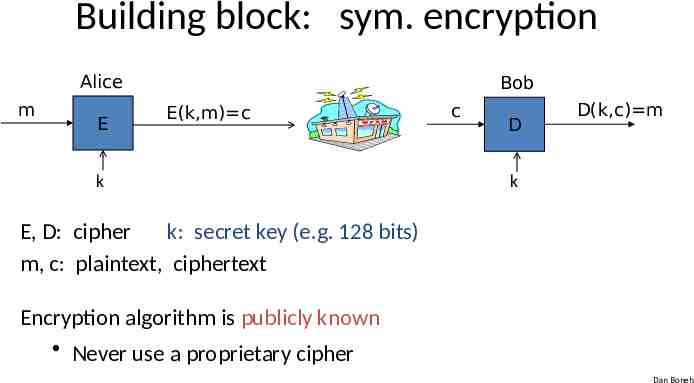
Building block: sym. encryption Alice m E Bob E(k,m) c k c D D(k,c) m k E, D: cipher k: secret key (e.g. 128 bits) m, c: plaintext, ciphertext Encryption algorithm is publicly known Never use a proprietary cipher Dan Boneh

Use Cases Single use key: (one time key) Key is only used to encrypt one message encrypted email: new key generated for every email Multi use key: (many time key) Key used to encrypt multiple messages encrypted files: same key used to encrypt many files Need more machinery than for one-time key Dan Boneh

Things to remember Cryptography is: – A tremendous tool – The basis for many security mechanisms Cryptography is not: – The solution to all security problems – Reliable unless implemented and used properly – Something you should try to invent yourself many many examples of broken ad-hoc designs Dan Boneh

End of Segment Dan Boneh

Online Cryptography Course Dan Boneh Introduction What is cryptography? Dan Boneh
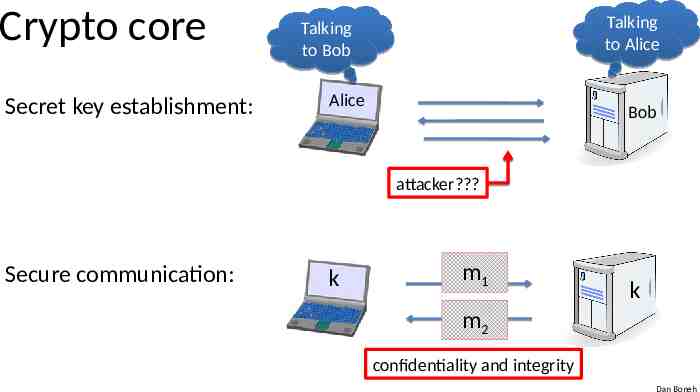
Crypto core Secret key establishment: Talking to Alice Talking to Bob Alice Bob attacker? Secure communication: k m1 k m2 confidentiality and integrity Dan Boneh
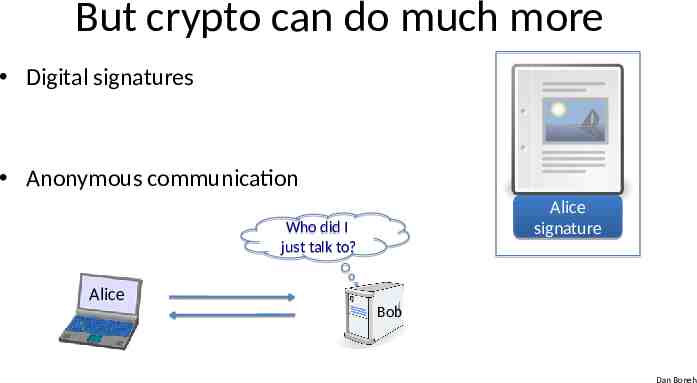
But crypto can do much more Digital signatures Anonymous communication Alice signature Who did I just talk to? Alice Bob Dan Boneh

But crypto can do much more Digital signatures Anonymous communication Anonymous digital cash – Can I spend a “digital coin” without anyone knowing who I am? – How to prevent double spending? 1 Alice Internet Who was that? (anon. comm.) Dan Boneh
Protocols Elections Private auctions Dan Boneh
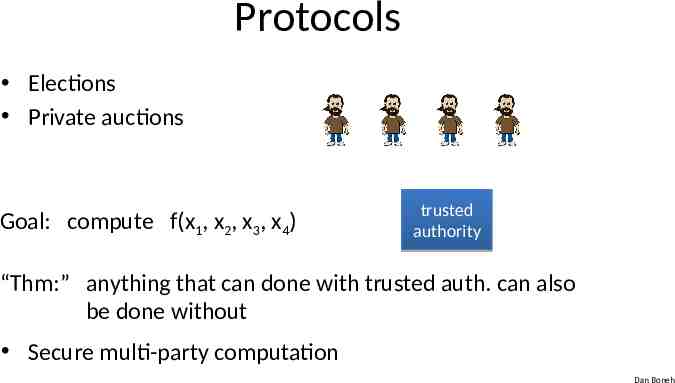
Protocols Elections Private auctions Goal: compute f(x1, x2, x3, x4) trusted authority “Thm:” anything that can done with trusted auth. can also be done without Secure multi-party computation Dan Boneh
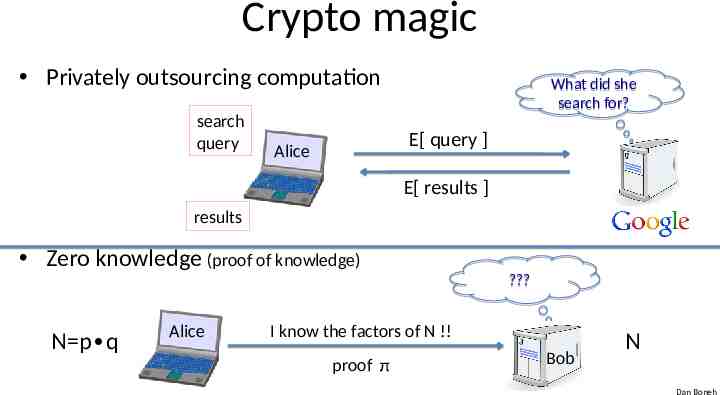
Crypto magic Privately outsourcing computation search query What did she search for? E[ query ] Alice E[ results ] results Zero knowledge (proof of knowledge) ? N p q Alice I know the factors of N !! proof π Bob N Dan Boneh

A rigorous science The three steps in cryptography: Precisely specify threat model Propose a construction Prove that breaking construction under threat mode will solve an underlying hard problem Dan Boneh

End of Segment Dan Boneh

Online Cryptography Course Dan Boneh Introduction History Dan Boneh

History David Kahn, “The code breakers” (1996) Dan Boneh
Symmetric Ciphers Dan Boneh
Few Historic Examples (all badly broken) 1. Substitution cipher k : Dan Boneh

Caesar Cipher (no key) Dan Boneh

What is the size of key space in the substitution cipher assuming 26 letters? ¿𝒦 26 26 factorial) ¿ 𝒦 2 26 ¿ 𝒦 26 2 Dan Boneh

How to break a substitution cipher? What is the most common letter in English text? “X” “L” “E” “H” Dan Boneh

How to break a substitution cipher? (1) Use frequency of English letters (2) Use frequency of pairs of letters (digrams) Dan Boneh
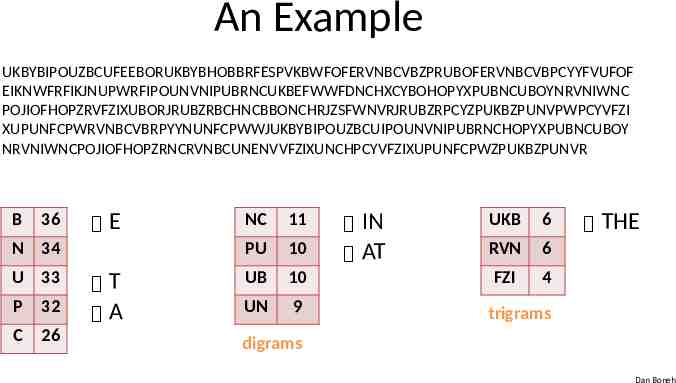
An Example UKBYBIPOUZBCUFEEBORUKBYBHOBBRFESPVKBWFOFERVNBCVBZPRUBOFERVNBCVBPCYYFVUFOF EIKNWFRFIKJNUPWRFIPOUNVNIPUBRNCUKBEFWWFDNCHXCYBOHOPYXPUBNCUBOYNRVNIWNC POJIOFHOPZRVFZIXUBORJRUBZRBCHNCBBONCHRJZSFWNVRJRUBZRPCYZPUKBZPUNVPWPCYVFZI XUPUNFCPWRVNBCVBRPYYNUNFCPWWJUKBYBIPOUZBCUIPOUNVNIPUBRNCHOPYXPUBNCUBOY NRVNIWNCPOJIOFHOPZRNCRVNBCUNENVVFZIXUNCHPCYVFZIXUPUNFCPWZPUKBZPUNVR B 36 E N 34 U 33 P 32 C 26 T A NC 11 PU 10 UB 10 UN 9 IN AT UKB 6 RVN 6 FZI 4 THE trigrams digrams Dan Boneh
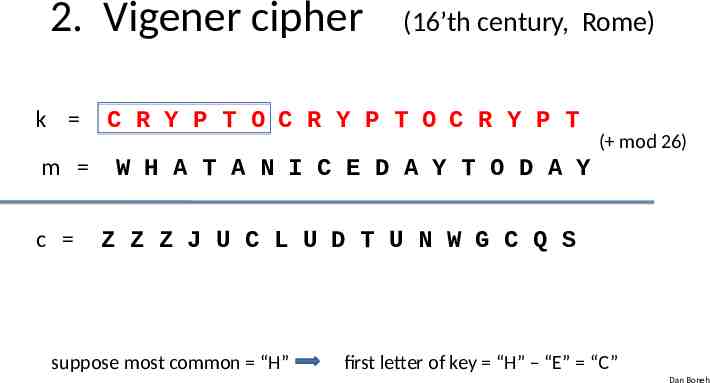
2. Vigener cipher k m c (16’th century, Rome) C R Y P T O C R Y P T O C R Y P T ( mod 26) W H A T A N I C E D A Y T O D A Y Z Z Z J U C L U D T U N W G C Q S suppose most common “H” first letter of key “H” – “E” “C” Dan Boneh
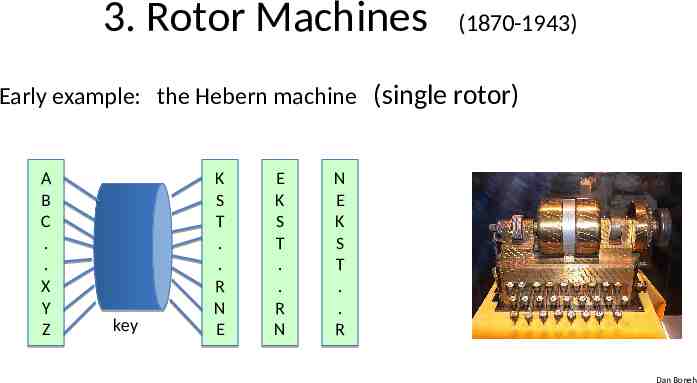
3. Rotor Machines (1870-1943) Early example: the Hebern machine (single rotor) A B C . . X Y Z key K S T . . R N E E K S T . . R N N E K S T . . R Dan Boneh

Rotor Machines (cont.) Most famous: the Enigma (3-5 rotors) # keys 264 218 (actually 236 due to plugboard) Dan Boneh

4. Data Encryption Standard DES: Today: (1974) # keys 256 , block size 64 bits AES (2001), Salsa20 (2008) (and many others) Dan Boneh

End of Segment Dan Boneh

Online Cryptography Course See also: Dan Boneh http://en.wikibooks.org/High School Mathematics Extensions/Discrete Probability Introduction Discrete Probability (crash course, cont.) Dan Boneh

U: finite set (e.g. U {0,1}n ) Def: Probability distribution P over U is a function P: U [0,1] such that Σ P(x) 1 x U Examples: 1. Uniform distribution: for all x U: P(x) 1/ U 2. Point distribution at x0: P(x0) 1, x x0: P(x) 0 Distribution vector: ( P(000), P(001), P(010), , P(111) ) Dan Boneh

Events For a set A U: Σ P(x) x A Pr[A] [0,1] note: Pr[U] 1 The set A is called an event Example: U {0,1}8 A { all x in U such that lsb2(x) 11 } U for the uniform distribution on {0,1}8 : Pr[A] 1/4 Dan Boneh
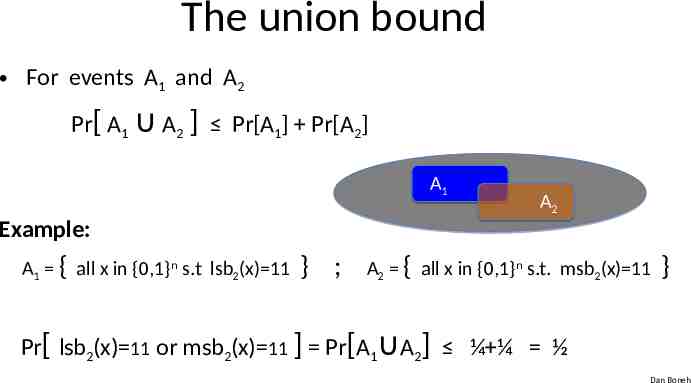
The union bound For events A1 and A2 Pr[ A1 A2 ] Pr[A1] Pr[A2] A1 A2 Example: A1 { all x in {0,1}n s.t lsb2(x) 11 } ; A2 { all x in {0,1}n s.t. msb2(x) 11 } Pr[ lsb2(x) 11 or msb2(x) 11 ] Pr[A1 A2] ¼ ¼ ½ Dan Boneh

Random Variables Def: a random variable X is a function Example: X: {0,1}n {0,1} ; X:U V X(y) lsb(y) {0,1} U For the uniform distribution on U: Pr[ X 0 ] 1/2 , V lsb 0 0 lsb 1 1 Pr[ X 1 ] 1/2 More generally: rand. var. X induces a distribution on V: Pr[ X v ] : Pr [ X-1(v) ] Dan Boneh

The uniform random variable Let U be some set, e.g. U {0,1}n R We write r U to denote a uniform random variable over U for all a U: Pr[ r a ] 1/ U ( formally, r is the identity function: r(x) x for all x U ) Dan Boneh

Let r be a uniform random variable on {0,1}2 Define the random variable X r1 r2 Then Pr[X 2] ¼ Hint: Pr[X 2] Pr[ r 11 ] Dan Boneh

Randomized algorithms inputs Deterministic algorithm: outputs y A(m) Randomized algorithm R n y A( m ; r ) where r {0,1} m A(m) output is a random variable y A( mR) Example: A(m ; k) E(k, m) , m A(m) R y A( m ) Dan Boneh

End of Segment Dan Boneh

Online Cryptography Course See also: Dan Boneh http://en.wikibooks.org/High School Mathematics Extensions/Discrete Probability Introduction Discrete Probability (crash course, cont.) Dan Boneh

Recap U: finite set (e.g. U {0,1}n ) Prob. distr. P over U is a function P: U [0,1] s.t. A U is called an event and Pr[A] Σ P(x) x A Σ P(x) 1 x U [0,1] A random variable is a function X:U V . X takes values in V and defines a distribution on V Dan Boneh

Independence Def: events A and B are independent if Pr[ A and B ] Pr[A] Pr[B] random variables X,Y taking values in V are independent if a,b V: Pr[ X a and Y b] Pr[X a] Pr[Y b] Example: U {0,1}2 {00, 01, 10, 11} Define r.v. X and Y as: X lsb(r) , and R r U Y msb(r) Pr[ X 0 and Y 0 ] Pr[ r 00 ] ¼ Pr[X 0] Pr[Y 0] Dan Boneh

Review: XOR XOR of two strings in {0,1}n is their bit-wise addition mod 2 0 1 1 0 1 1 1 1 0 1 1 0 1 0 Dan Boneh

An important property of XOR Thm: Y a rand. var. over {0,1}n , X an indep. uniform var. on {0,1}n Then Z : Y X is uniform var. on {0,1}n Proof: (for n 1) Pr[ Z 0 ] Dan Boneh

The birthday paradox Let r1, , rn U be indep. identically distributed random vars. Thm: when n 1.2 U 1/2 then Pr[ i j: ri rj ] ½ notation: U is the size of U Example: Let U {0,1}128 After sampling about 264 random messages from U, some two sampled messages will likely be the same Dan Boneh
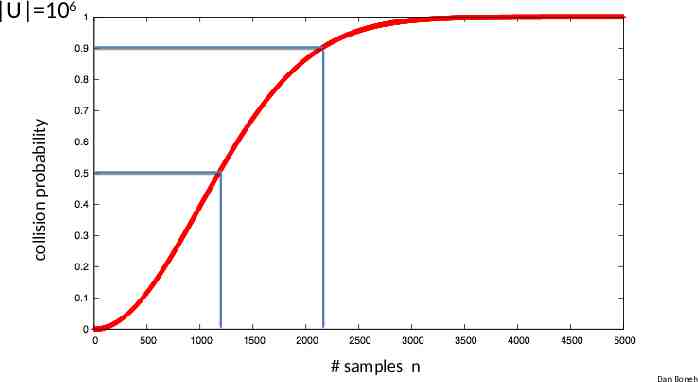
collision probability U 106 # samples n Dan Boneh

End of Segment Dan Boneh






