Lecture 6: Schema refinement: Functional dependencies
30 Slides295.00 KB

Lecture 6: Schema refinement: Functional dependencies www.cl.cam.ac.uk/Teaching/current/Databases/ 1

Recall: Database design lifecycle Requirements analysis – User needs; what must database do? Conceptual design – High-level description; often using E/R model Logical design – Translate E/R model into relational schema Schema refinement – Check schema for redundancies and anomalies Next two lectures Physical design/tuning – Consider typical workloads, and further optimise 2

Today’s lecture Why are some designs bad? What’s a functional dependency? What’s the theory of functional dependencies? (Next lecture: How can we use this theory to classify redundancy in relation design?) 3

Not all designs are equally good Why is this design bad? Data(sid,sname,address,cid,cname,grade) Why is this one preferable? Student(sid,sname,address) Course(cid,cname) Enrolled(sid,cid,grade) 4
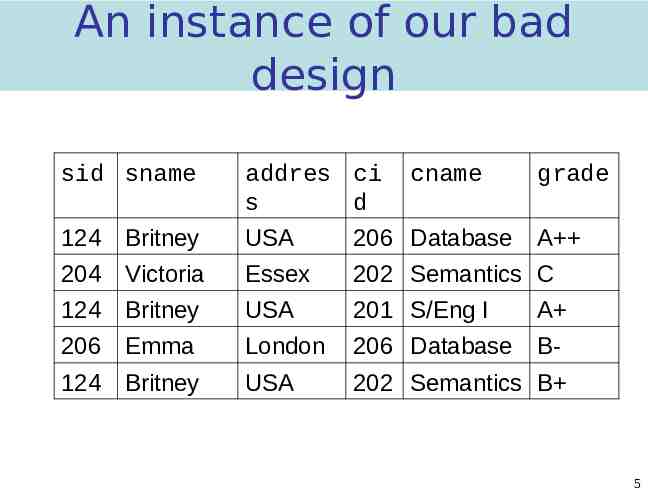
An instance of our bad design sid sname addres ci s d cname grade 124 Britney USA 206 Database 204 Victoria Essex 202 Semantics C 124 Britney USA 201 S/Eng I A 206 Emma London 206 Database B- 124 Britney USA 202 Semantics B A 5

Evils of redundancy Redundancy is the root of many problems associated with relational schemas – Redundant storage – Update anomalies – Insertion anomalies – Deletion anomalies – LOW TRANSACTION THROUGHPUT In general, with higher redundancy, if transactions are correct (no anomalies), then they have to lock more objects thus causing greater contention and lower throughput (Aside: Could having a dummy value, NULL, help?) 6

Decomposition We remove anomalies by replacing the schema Data(sid,sname,address,cid,cname,grade) with Student(sid,sname,address) Course(cid,cname) Enrolled(sid,cid,grade) Note the implicit extra cost here Two immediate questions: 1. Do we need to decompose a relation? 2. What problems might result from a decomposition? 7

Functional dependencies Recall: – A key is a set of fields where if a pair of tuples agree on a key, they agree everywhere In our bad design, if two tuples agree on sid, then they also agree on address, even though the rest of the tuples may not agree 8

Functional dependencies cont. We can say that sid determines address – We’ll write this sid address This is called a functional dependency (FD) (Note: An FD is just another integrity constraint) 9

Functional dependencies cont. We’d expect the following functional dependencies to hold in our Student database – sid sname,address – cid cname – sid,cid grade A functional dependency X Y is simply a pair of sets (of field names) – Note: the sloppy notation A,B C,D rather than {A,B} {C,D} 10

Formalities Given a relation R R(A1: 1, , An: n), and X, Y ( {A1, , An}), an instance r of R satisfies X Y, if – For any two tuples t1, t2 in R, if t1.X t2.X then t1.Y t2.Y Note: This is a semantic assertion. We can not look at an instance to determine which FDs hold (although we can tell if the instance does not satisfy an FD!) 11

Properties of FDs Assume that X Y and Y Z are known to hold in R. It’s clear that X Z holds too. We shall say that an FD set F logically implies X Y, and write F [X Y – e.g. {X Y, Y Z} [ X Z The closure of F is the set of all FDs logically implied by F, i.e. F @ {X Y F [ X Y} The set F can be big, even if F is small 12

Closure of a set of FDs Which of the following are in the closure of our Student FDs? – address address – cid cname – cid cname,sname – cid,sid cname,sname 13

Candidate keys and FDs If R R(A1: 1, , An: n) with FDs F and X {A1, , An}, then X is a candidate key for R if – X A1, ,An F – For no proper subset Y X is Y A1, ,An F 14

Armstrong’s axioms Reflexivity: If Y X then F \ X Y – (This is called a trivial dependency) – Example: sname,address address Augmentation: If F \ X Y then X,W Y,W F\ – Example: As cid cname then cid,sid cname,sid Transitivity: If F \ X Y and F \ Y Z then F \ X Z – Example: As sid,cid cid and cid cname, then sid,cid cname 15

Consequences of Armstrong’s axioms Union: If F \ X Y and F \ X Z then F\ X Y,Z Pseudo-transitivity: If F \ X Y and F\ W,Y Z then F \ X,W Z Decomposition: If F \ X Y and Z Y then F \ X Z Exercise: Prove that these are consequences of Armstrong’s axioms 16

Proof of Union Rule Suppose that F \ X Y and F \ X Z. By augmentation we have F \ X X,Y since X U X X. Also by augmentation F \ X,Y Z,Y Therefore, by transitivity we have F \ X Z,Y QED 17

Functional Dependencies Can be useful in Algebraic Reasoning Suppose R(A,B,C) is a relation schema with dependency A B, then R π A, B ( R ) A π A ,C ( R ) (This is called Heath’s rule.) 18

Proof of Heath’s Rule First show that A π A ,C ( R ) Suppose then and Since we have A π A ,C ( R ) 19

Proof of Heath’s Rule (cont.) In the other direction, we must show that A Suppose Then there must exist records and There must also exist so that But the functional dependency tells us that Therefore, we have QED 20

Equivalence Two sets of FDs, F and G, are said to be equivalent if F G For example: {(A,B C), (A B)} and {(A C), (A B)} are equivalent F can be huge – we’d prefer to look for small equivalent FD sets 21

Minimal cover An FD set, F, is said to be minimal if 1. Every FD in F is of the form X A, where A is a single attribute 2. For no X A in F is F-{X A} equivalent to F 3. For no X A in F and Z X is (F-{X A}) {Z A} equivalent to F 1. For example, {(A C), (A B)} is a minimal cover for {(A,B C), (A B)} 22

More on closures FACT: If F is an FD set, and X Y F then there exists an attribute A Y such that X A F 23

Why Armstrong’s axioms? Soundness – If F \ X Y is deduced using the rules, then X Y is true in any relation in which the dependencies of F are true Completeness – If X Y is is true in any relation in which the dependencies of F are true, then F \ X Y can be deduced using the rules 24

Soundness Consider the Augmentation rule: – We have X Y, i.e. if t1.X t2.X then t1.Y t2.Y – If in addition t1.W t2.W then it is clear that t1. (Y,W) t2.(Y,W) 25

Soundness cont. Consider the Transitivity rule: – We have X Y, i.e. if t1.X t2.X then t1.Y t2.Y (*) – We have Y Z, i.e. if t1.Y t2.Y then t1.Z t2.Z (**) – Take two tuples s1 and s2 such that s1.X s2.X then from (*) s1.Y s2.Y and then from (**) s1.Z s2.Z 26

Completeness Exercise – (You may need the fact from slide 23) 27

Attribute closure If we want to check whether X Y is in a closure of the set F, could compute F and check – but expensive Cheaper: We can instead compute the attribute closure, X , using the following algorithm: closure: X; repeat until no change{ if U V F, where U closure then closure: closure V }; Then F \ X Y iff Y is a subset of X Try this with sid,sname cname,grade 28

Preview of next lecture: Goals of normalisation Decide whether a relation is in “good form” If it is not, then we will “decompose” it into a set of relations such that – Each relation is in “good form” – The decomposition has not lost any information that was present in the original relation The theory of this process and the notion of “good form” is based on FDs 29

Summary You should now understand: Redundancy and various forms of anomalies Functional dependencies Armstrong’s axioms Next lecture: Schema refinement: Normalisation 30