Introduction to Algorithms (2nd edition) by Cormen, Leiserson, Rivest
24 Slides975.00 KB

Introduction to Algorithms (2nd edition) by Cormen, Leiserson, Rivest & Stein Chapter 2: Getting Started (slides enhanced by N. Adlai A. DePano)

Overview Aims to familiarize us with framework used throughout text Examines alternate solutions to the sorting problem presented in Ch. 1 Specify algorithms to solve problem Argue for their correctness Analyze running time, introducing notation for asymptotic behavior Introduce divide-and-conquer algorithm technique

The Sorting Problem Input: A sequence of n numbers [a1, a2, , an]. Output: A permutation or reordering [a'1, a'2, , a'n ] of the input sequence such that a'1 a'2 a'n . An instance of the Sorting Problem: Input: A sequence of 6 number [31, 41, 59, 26, 41, 58]. Expected output for given instance: Expected Output: The permutation of the input [26, 31, 41, 41, 58 , 59].
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Insertion Sort The main idea
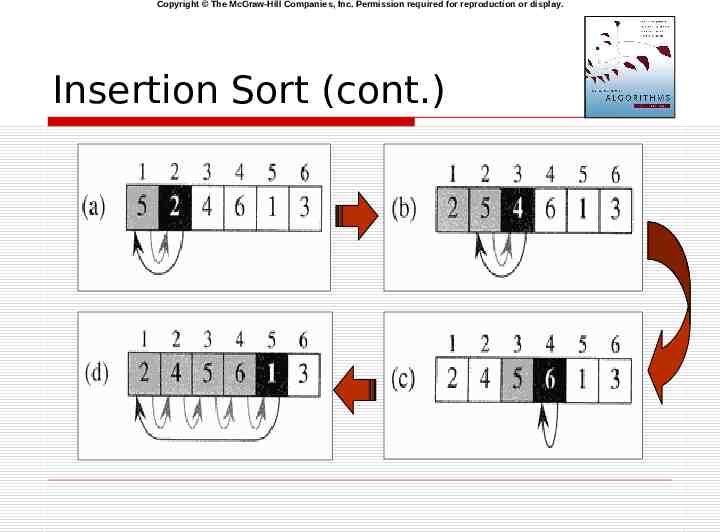
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Insertion Sort (cont.)
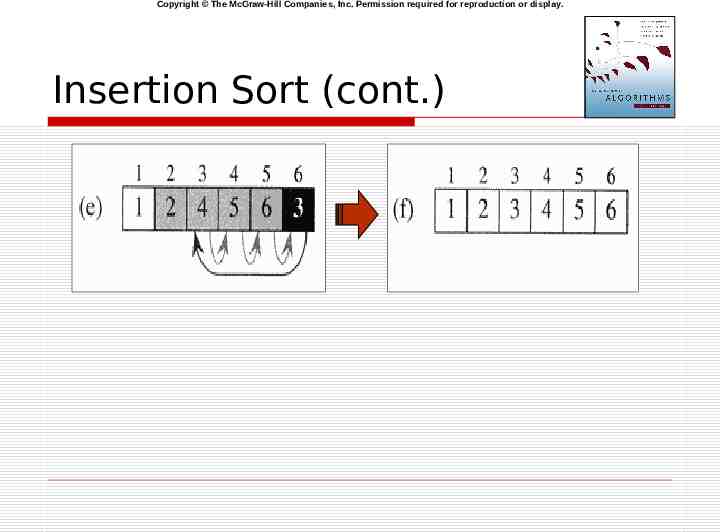
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Insertion Sort (cont.)

Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Insertion Sort (cont.) The algorithm

Loop Invariant Property of A[1 . j 1] At the start of each iteration of the for loop of lines 1 8, the subarray A[1 . j 1] consists of the elements originally in A[1 . j 1] but in sorted order. Need to establish the following re invariant: Initialization: true prior to first iteration Maintenance: if true before iteration, remains true after iteration Termination: at loop termination, invariant implies correctness of algorithm

Analyzing Algorithms Has come to mean predicting the resources that the algorithm requires Usually computational time is resource of primary importance Aims to identify best choice among several alternate algorithms Requires an agreed-upon “model” of computation Shall use a generic, one-processor, randomaccess machine (RAM) model of computation

Random-Access Machine Instructions are executed one after another (no concurrency) Admits commonly found instructions in “real” computers, data movement operations, control mechanism Uses common data types (integer and float) Other properties discussed as needed Care must be taken since model of computation has great implications on resulting analysis

Analysis of Insertion Sort Time resource requirement depends on input size Input size depends on problem being studied; frequently, this is the number of items in the input Running time: number of primitive operations or “steps” executed for an input Assume constant amount of time for each line of pseudocode

Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Analysis of Insertion Sort Time efficiency analysis

Best Case Analysis Least amount of (time) resource ever needed by algorithm Achieved when incoming list is already sorted in increasing order Inner loop is never iterated Cost is given by: T(n) c1n c2 (n 1) c4 (n 1) c5(n 1) c8(n 1) (c1 c2 c4 c5 c8)n (c2 c4 c5 c8) an b Linear function of n

Worst Case Analysis Greatest amount of (time) resource ever needed by algorithm Achieved when incoming list is in reverse order Inner loop is iterated the maximum number of times, i.e., tj j Therefore, the cost will be: T(n) c1n c2 (n 1) c4 (n 1) c5((n(n 1)/2) 1) c6(n(n 1)/2) c7(n(n 1)/2) c8(n 1) ( c5 /2 c6 /2 c7/2 ) n2 (c1 c2 c4 c5 /2 c6 /2 c7 /2 c8 ) n ( c2 c4 c5 c8 ) an2 bn c Quadratic function of n

Future Analyses For the most part, subsequent analyses will focus on: Worst-case running time Upper bound on running time for any input Average-case analysis Expected running time over all inputs Often, worst-case and average-case have the same “order of growth”

Order of Growth Simplifying abstraction: interested in rate of growth or order of growth of the running time of the algorithm Allows us to compare algorithms without worrying about implementation performance Usually only highest order term without constant coefficient is taken Uses “theta” notation Best case of insertion sort is (n) Worst case of insertion sort is (n2)

Designing Algorithms Several techniques/patterns for designing algorithms exist Incremental approach: builds the solution one component at a time Divide-and-conquer approach: breaks original problem into several smaller instances of the same problem Results in recursive algorithms Easy to analyze complexity using proven techniques

Divide-and-Conquer Technique (or paradigm) involves: “Divide” stage: Express problem in terms of several smaller subproblems “Conquer” stage: Solve the smaller subproblems by applying solution recursively – smallest subproblems may be solved directly “Combine” stage: Construct the solution to original problem from solutions of smaller subproblem
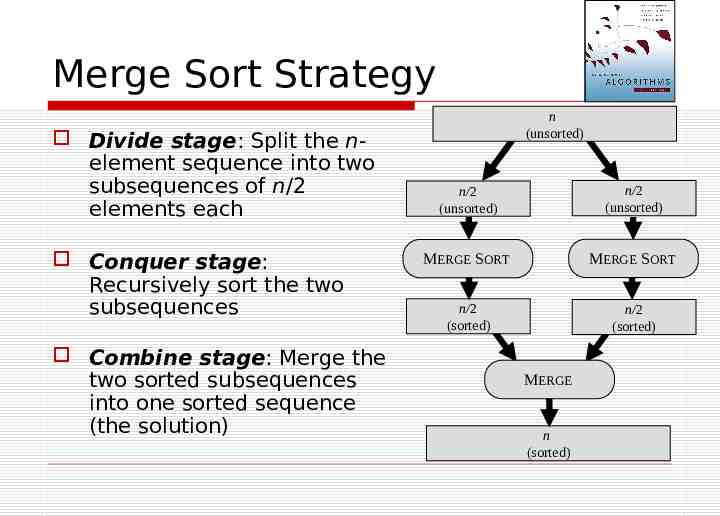
Merge Sort Strategy Divide stage: Split the nelement sequence into two subsequences of n/2 elements each Conquer stage: Recursively sort the two subsequences Combine stage: Merge the two sorted subsequences into one sorted sequence (the solution) n (unsorted) n/2 (unsorted) n/2 (unsorted) MERGE SORT MERGE SORT n/2 (sorted) n/2 (sorted) MERGE n (sorted)
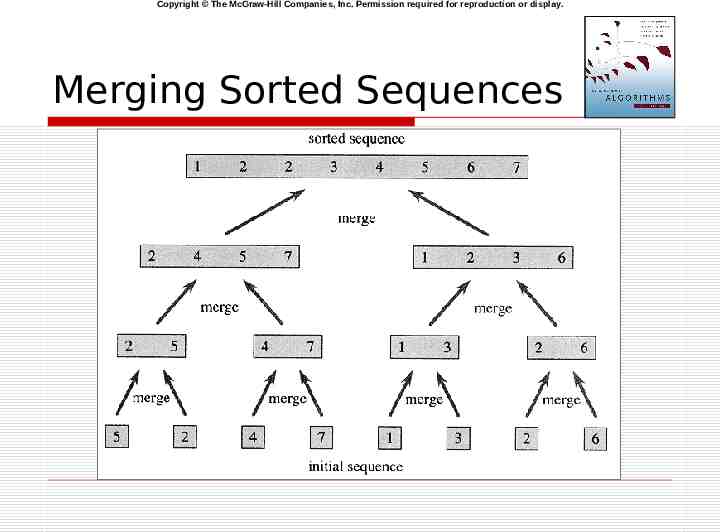
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Merging Sorted Sequences

Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Merging Sorted Sequences Combines the sorted (1) (n) (1) subarrays A[p.q] and A[q 1.r] into one sorted array A[p.r] Makes use of two working arrays L and R which initially hold copies of the two subarrays Makes use of sentinel (n) value ( ) as last element to simplify logic

Merge Sort Algorithm (1) T(n/2) T(n/2) (n) T(n) 2T(n/2) (n)
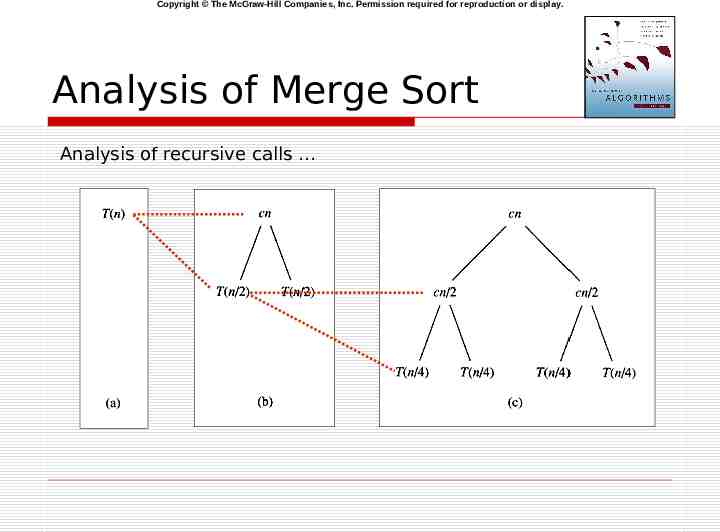
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Analysis of Merge Sort Analysis of recursive calls
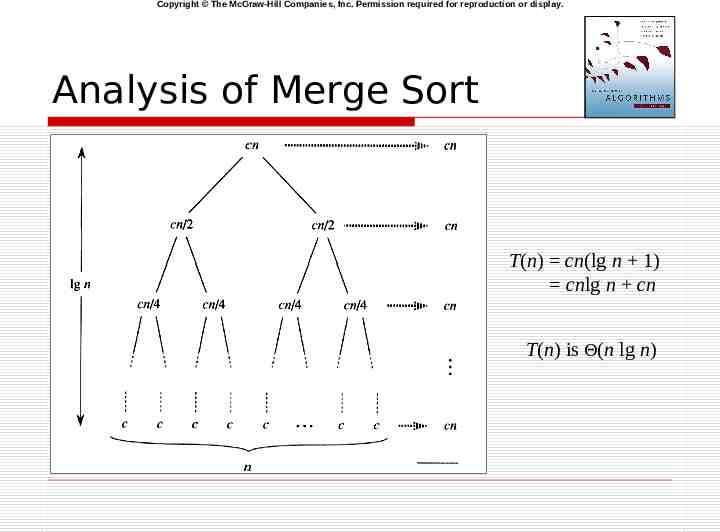
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Analysis of Merge Sort T(n) cn(lg n 1) cnlg n cn T(n) is (n lg n)






