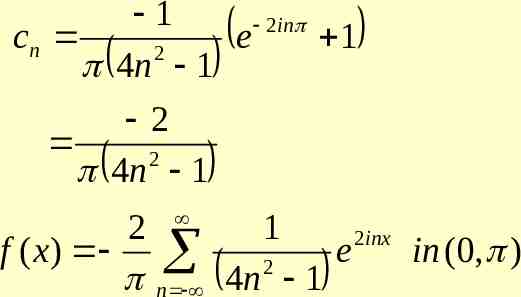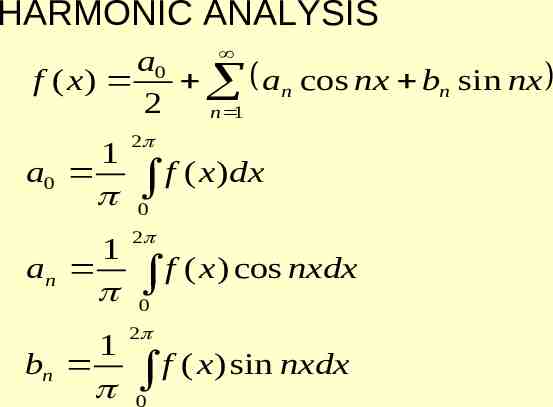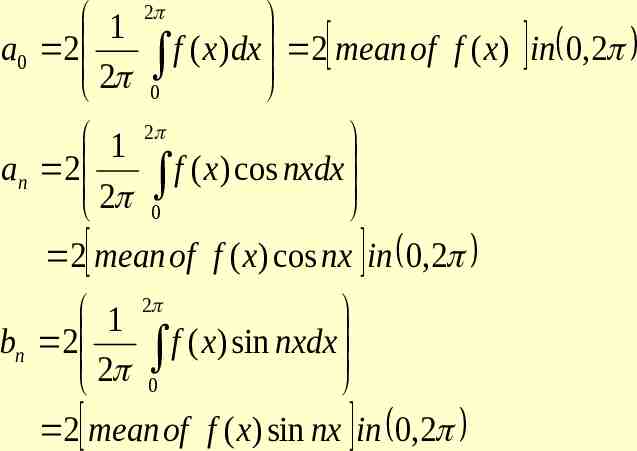FOURIER SERIES PERIODIC FUNCTIONS A function f(x) is said to
81 Slides1.36 MB

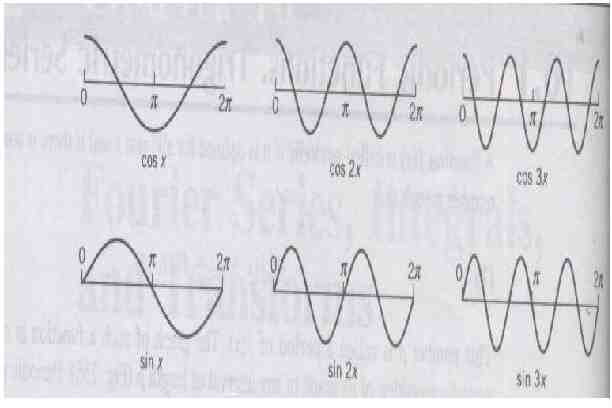
FOURIER SERIES PERIODIC FUNCTIONS A function f(x) is said to be periodic with period T if f(x T) f(x) x , where T is a positive constant . The least value of T 0 is called the period of f(x).

f(x 2T) f ((x T) T) f (x T) f(x) f(x nT) f(x) for all x Ex.1 f(x) sin x has periods 2 , 4 , 6 , . and 2 is the period of f(x). Ex.2 The period of sin nx and cos nx is 2 /n.
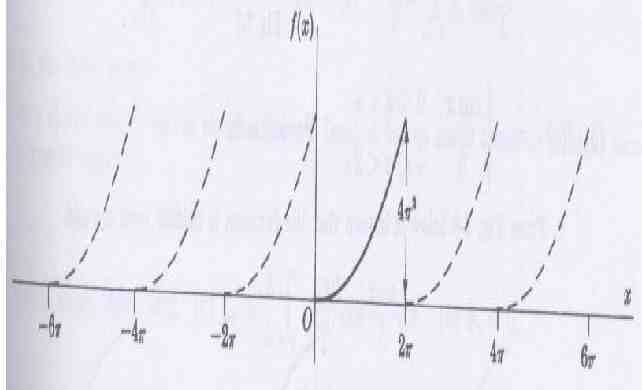
FOURIER SERIES f (xdefined ) Let be in the interval and outside ( l , l ) the interval by x 2l ) f has ( x) the i.e assumef (that f (x) period .The Fourierseries 2l corresponding to is given by f (x ) a0 n x n x an cos bn sin 2 n 1 l l

where the Fourier coeffecients are l a0 1 f ( x ) dx l l l an 1 n x f ( x ) cos dx l l l l bn 1 n x f ( x ) sin dx l l l n 1,2,3,.

) defined in the interval If f (xis (c,c 2 ),lthe coefficients can be determined equivalently from a0 an bn 1 l c 2l 1 l c 2l 1 l c 2l f ( x ) dx c c c n x f ( x ) cos dx l n x f ( x ) sin dx l

DIRICHLET CONDITIONS Suppose that 1.f(x) is defined and single valued except possibly at finite number of points in (-l, l) 2.f(x) is periodic outside (-l, l) with period 2l 3.f(x) and f’(x) are piecewise continuous in(-l, l)

Then the Fourier series of f(x) converges to a)f(x) if x is a point of continuity b)[f(x 0) f(x-0)]/2 if x is a point of discontinuity

METHOD OF OBTAINING FOURIER SERIES OF f (x ) a0 n x n x 1. f (x ) 2 an cos l bn sin l n 1 l 2. a0 1 f ( x ) dx l l l 3. an 1 n x f ( x ) cos dx l l l 4. bn 1 n x f ( x ) sin dx l l l l n 1,2,3,.

SOLVED PROBLEMS 1. Expand f(x) x2,0 x 2 in Fourier series 2 1 1 1 if the period is 2 . Prove that . 12 22 32 6

SOLUTION Period 2 l 2 thus l and choosing c 0 1 an l c 2 1 1 c n x f ( x ) cos dx l 2 f ( x) cos nx dx 0 2 2 x cos nx dx 0 2 1 2 sin nx cos nx sin nx x 2 x 2 2 3 n n n 0 4 2 n 0 n
2 2 8 a0 x 2 dx 0 3 1 1 bn l 1 1 c 2 c n x f ( x ) sin dx l 2 f ( x) sin nxdx 0 2 2 x sin nxdx 0 2 1 2 cos nx cos nx sin nx x 2 x 2 2 n n n 3 0 4 n
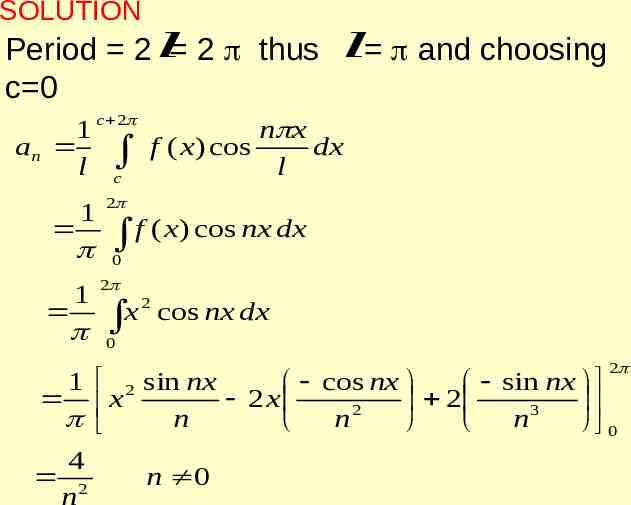
a0 f ( x) an cos nx bn sin nx 2 n 1 2 4 4 4 2 f ( x) x 2 cos nx sin nx 3 n 1 n n At x 0 the above Fourier series reduces to 4 2 4 3 n 1 n2 X 0 is the point of discontinuity
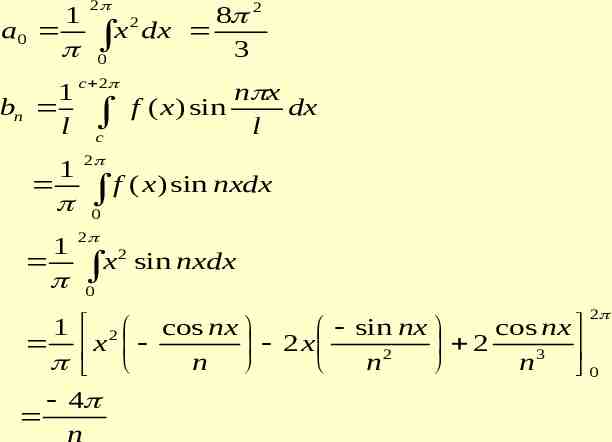
By Dirichlet conditions, the series converges at x 0 to (0 4 2)/2 2 2 2 n 1 2 4 2 4 2 3 n 1 n 1 2 2 n 6

2. Find the Fourier series expansion for the following periodic function of period 4. Solution 2 x 2 x 0 f ( x) 2 x 0 x 2 f ( x 4) f ( x ) l a0 1 f ( x ) dx l l 0 2 1 2 x dx 2 x dx 2 2 0 0 2 1 x2 x2 2x 2x 2 2 2 2 0 2
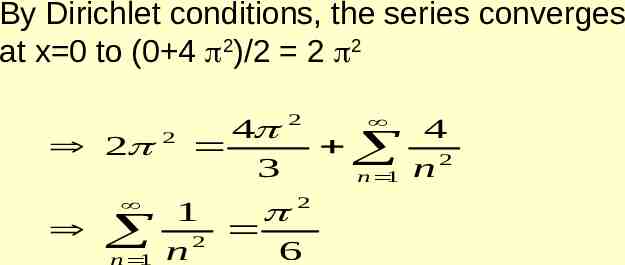
l an 1 n x f ( x ) cos dx l l l 0 2 1 n n 2 x cos xdx 2 x cos xdx 2 2 2 2 0 n x n x sin cos 1 2 (1) 2 2 x 2 n ( n ) 2 2 4 0 2 n x n x sin cos 2 ( 1) 2 2 x 2 n ( n ) 2 4 4 2 2 1 ( 1) n n 0 for n even 8 for n odd 2 2 n 2 0

l 1 n x bn f ( x ) sin dx l l l 0 2 1 n x n x 2 x sin dx 2 x sin dx 2 2 l l 0 0 n x n x cos sin 1 2 2 2 x ( 1 ) 2 2 n n 2 2 4 2 n x cos 2 2 x n 2 f ( x ) 1 8 2 n 1 2 n x sin 2 ( 1) 0 2 2 n 4 0 1 x cos 2 n 1 n 2 2
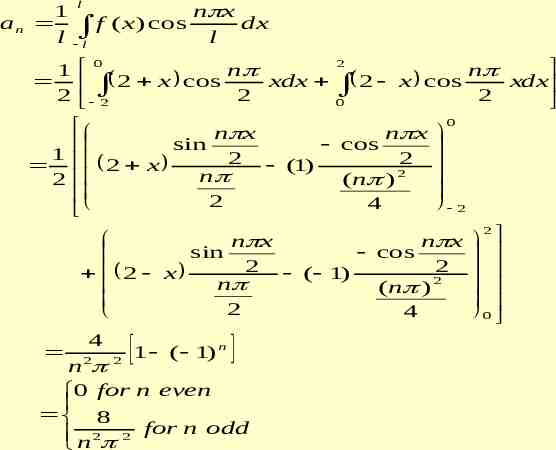
EVEN AND ODD FUNCTIONS A function f(x) is called odd if f(-x) -f(x) Ex: x3, sin x, tan x,x5 2x 3 A function f(x) is called even if f(-x) f(x) Ex: x4, cos x,ex e-x,2x6 x2 2
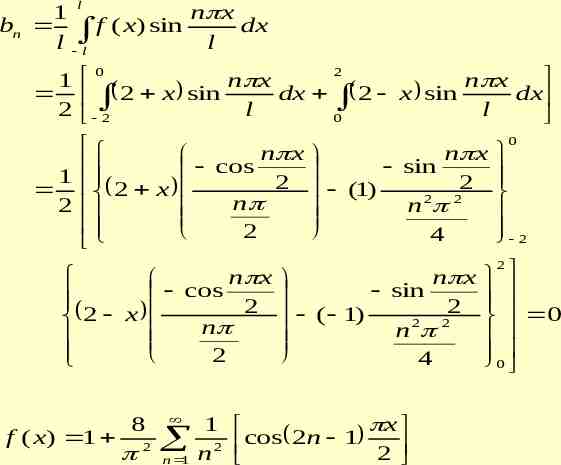
EXPANSIONS OF EVEN AND ODD PERIODIC FUNCTIONS If f (x) is a periodic function defined in the interval ( l , l ) , it can be represented by the Fourier series Case1. If f (x) is an even function l a0 1 f ( x )dx l l 2 l l f ( x )dx 0

l 2 n x an f ( x) cos dx l 0 l n x is also even function f ( x) cos l l 1 n x bn f ( x) sin dx l l l n x 0 f ( x) sin is odd function l (x) in If a periodic function isf even ( l , l ) , its Fourier series expansion contains only cosine terms

a0 n x f ( x) an cos 2 l n 1 a0 an 2 l 2 l l f ( x)dx 0 l n x f ( x ) cos dx l 0 Case 2. When f (x) is an odd function l 1 a0 f ( x ) dx 0 l l
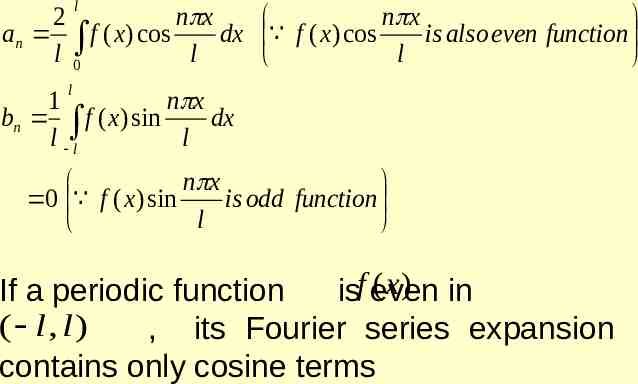
l 1 n x n x an f ( x) cos dx 0 f ( x) cos is odd l l l l l 2 n x n x bn f ( x) sin dx f ( x) sin is even l0 l l (x ) in If a periodic function isf odd ( l , l ),its Fourier expansion contains only sine terms n x f ( x ) bn sin n 1 2 bn l l l n x f ( x ) sin dx l 0
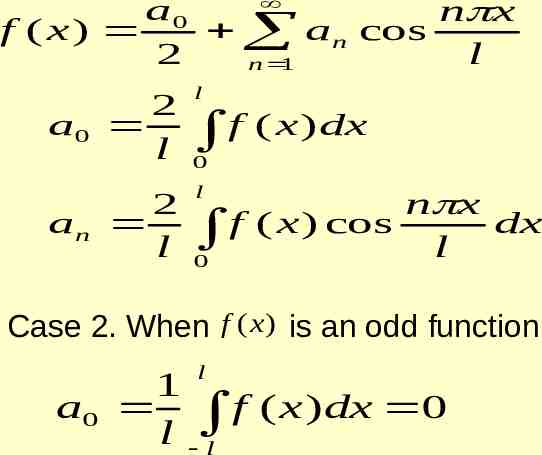
SOLVED PROBLEMS 1.For a function defined by f ( x) x , x obtain a Fourier series. Deduce that 1 1 1 2 2 2 . 2 1 3 5 8 Solution f ( x ) x is an even function a0 n x f ( x) an cos 2 l n 1
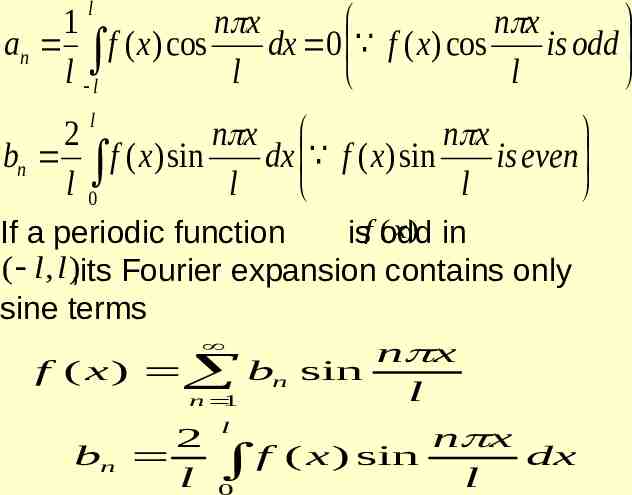
SOLUTION a0 2 x dx 0 2 2 2 2 x xdx 0 2 0 an 2 x cos nxdx x cos nxdx 0 0 2 sin nx cos nx x 2 n n 0 2 n 1 1 2 n

f ( x) 2 2 1 n 1 n cos nx 1 n2 At x 0 the above series reduces to n 2 1 1 2 n 1 n2 x 0 is a point of continuity, by Dirichlet condition the Fourier series converges to f(0) and f(0) 0
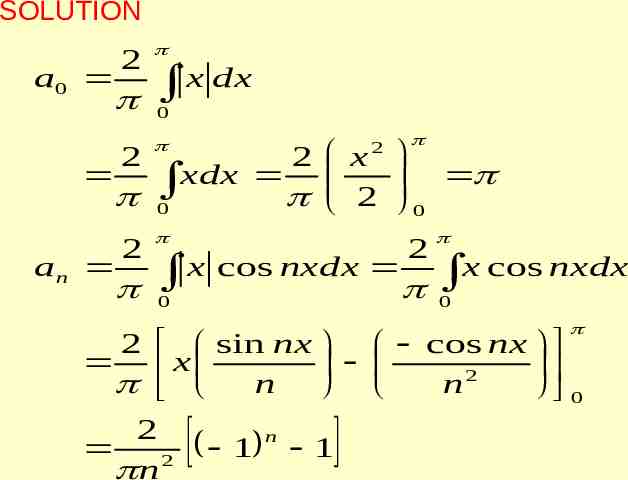
0 0 2 2 2 2 1 n 1 2 n n 1 2 2 2 2 2 2 . 3 5 1 2 1 1 1 2 2 . 2 1 3 5 8 k when 3 x 0 f ( x) k when 0 x 3 Is the function even or odd. Find the Fourier series of f(x) PROBLEM 2
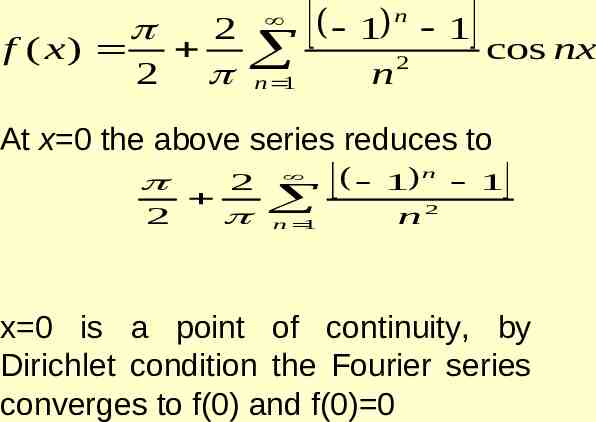
SOLUTION f (x ) is odd function a0 0 bn 2 l 2 3 an 0 l n x f ( x ) sin dx l 0 3 n x k sin dx 3 0

n x k cos 2 3 n 3 3 2k [1 ( 1) n ] n n 3 0 2k [1 ( 1) ] n x f ( x) sin n 1 n 3
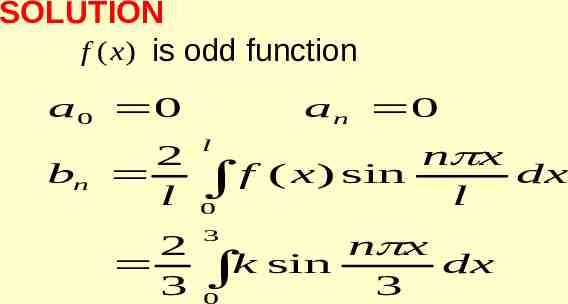
n x k cos 2 3 n 3 3 2k [1 ( 1) n ] n n 3 0 2k [1 ( 1) ] n x f ( x) sin n 1 n 3
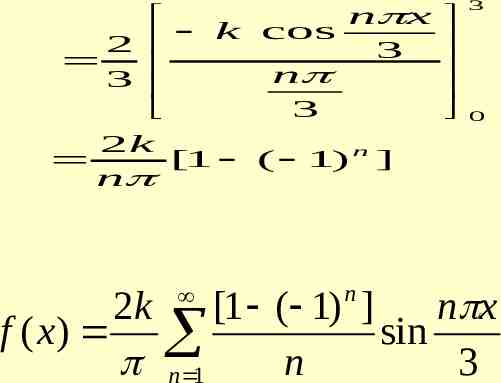
n x k cos 2 3 n 3 3 2k [1 ( 1) n ] n n 3 0 2k [1 ( 1) ] n x f ( x) sin n 1 n 3
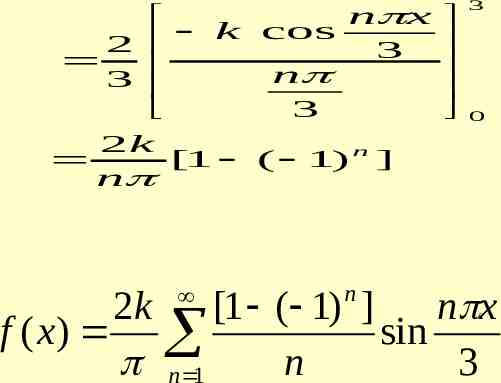
HALF RANGE SERIES COSINE SERIES A function f (x) defined in (0, l ) can be expanded as a Fourier series of period 2l containing only cosine terms by extending f (x) suitably in ( l ,0) . (As an even function) a0 n x f ( x) an cos 2 l n 1 where 2 an l l n x f ( x ) cos dx, n 0 l 0
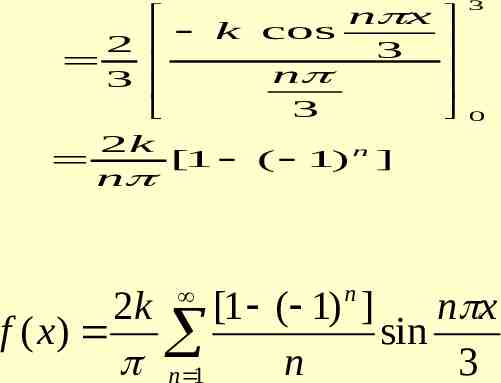
SINE SERIES A function f (x) defined in (0, l ) can be expanded as a Fourier series of period 2l containing only sine terms by extending f (x ) suitably in ( l ,0). [As an odd function] n x f ( x ) bn sin l u 1 where bn 2 l l n x f ( x ) sin dx, n 1 l 0

SOLVED PROBLEMS Obtain the Fourier expansion of (x sinx )as a cosine series in (0, ) .Hence find the value of 1 2 2 2 1 .3 3.5 5.7 SOLUTION ( , ) Given function represents an even function in a0 f ( x) an cos nx 2 n 1

2 an f 0 2 a 0 ( x) cos nxdx f ( x)dx 0 2 2 a x sin xdx x( cos x) 1( sin x) 0 0 0 2 2 an x sin x cos nxdx 0

2 1 x sin(1 n) x sin(1 n) x dx 0 2 cos(1 n) x sin(1 n) x x 1. 2 1 n (1 n) 0 1 sin(1 n) x cos(1 n) x x 1. 2 1 n (1 n) 0
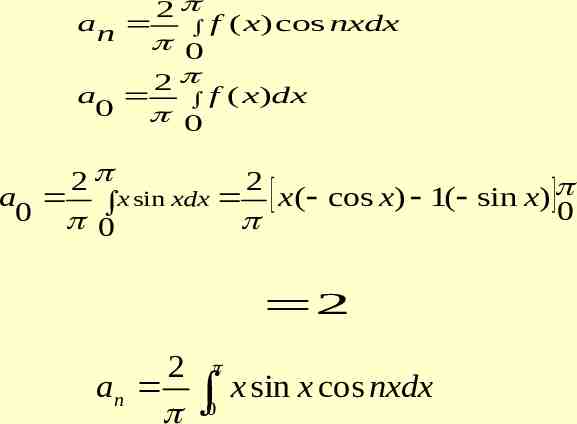
n 1 1( 1) n 1 1 1 n ( 1) n 1 n 1 1 2 1 1 ( 1) 2 n 1 n 1 n 1 n 1 n 1 if n 1
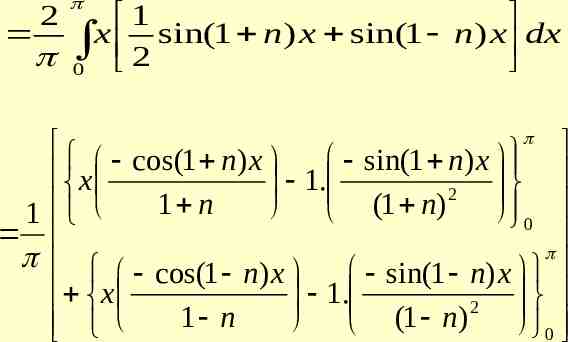
2 1 a1 x sin x cos xdx x sin 2 xdx 0 0 1 cos 2 x sin 2 x 1. x 2 2 2 0 1 1 2 2 1 ( 1) n 1 x sin x 1 cos x 2 2 cos nx 2 n 2 n 1 in (0, )
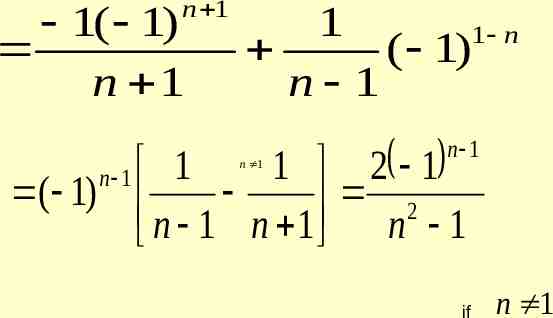
x At 2 1 2 n 2 x 2 the above series reduces to 1 n 2 n 1 n cos 1 2 is a point of continuity The given series converges to f( ) 2 2
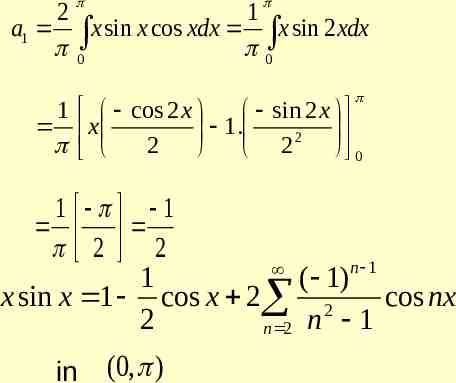
2 1 2 n 2 1 n 2 n 1 n cos 1 2 1 1 1 2 . 1.3 3.5 5.7 4
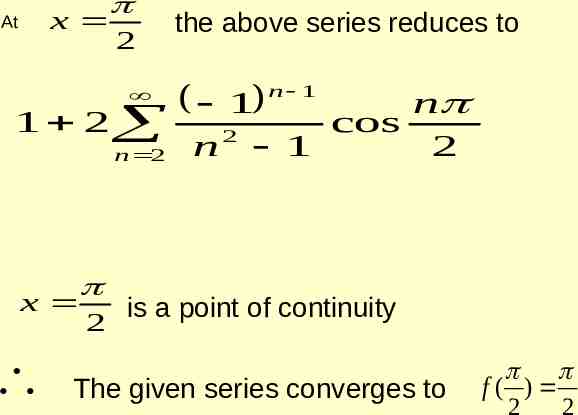
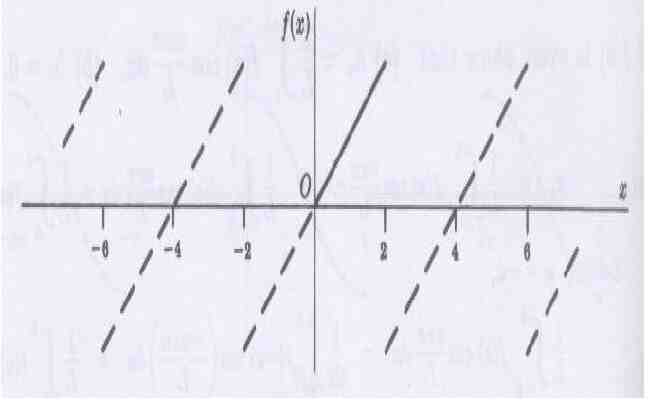
2) Expand f ( x ) x, 0 x 2 in half range (a) sine Series (b) Cosine series. SOLUTION (a) Extend the definition of given function to that of an odd function of period 4 i.e x; 2 x 0 f ( x) x; 0 x 2
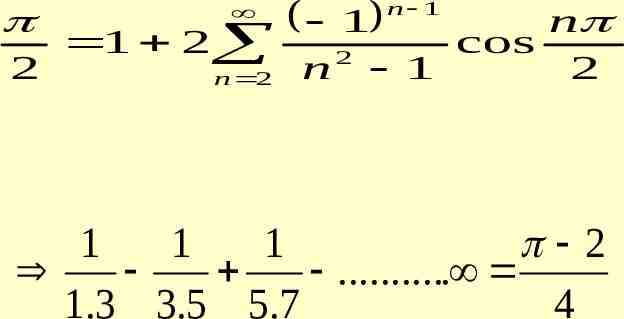
an 0 Here l 2 n x bn f ( x) sin dx l 0 l 2 2 n x bn f ( x) sin dx 20 2 2 n x n x sin n cos 2 4 ( 1 ) 2 ) x ( ) 1( 2 2 n n n 2 0 2 2

f ( x) 4 n 1 ( 1) n n x sin n 2 (b) Extend the definition of given function to that of an even function of period 4 x; 2 x 0 f ( x) x;0 x 2
bn 0 l 2 2 n x an f ( x) cos dx l 0 l n x 2 an f ( x) cos dx 20 2 2 n x n x cos n sin 2 4 ( 1 ) 1 2 x ( ) 1( ) ; 2 2 2 2 n n n 2 0 2 2 n 0
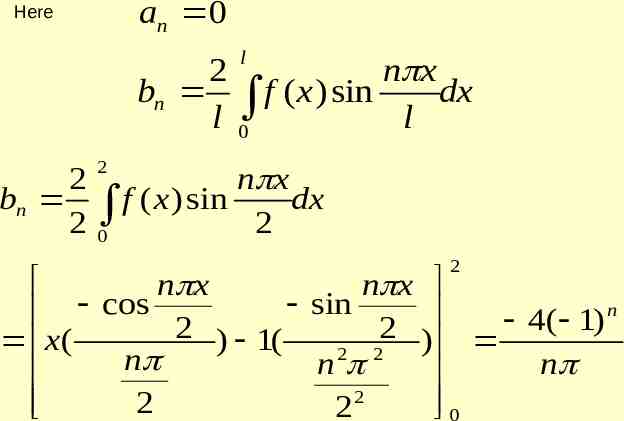
2 a0 xdx 2 0 4 f ( x) 1 2 n 1 ( 1) n n 2 cos n x 1 2

Exercise problems 1. 0; x o f ( x) sin x;0 x f (x ) Find Fourier series of 2. f (x ) e x in (0,2 ) Find Fourier series of f (x )
3.Find the Fourier series of in ( , ) 4.Find the Fourier series of in f ( x) x 3 (-2 ,2) f ( x) 4 x 2
5.Represent function x f ( x) sin L In (0,L) by a Fourier cosine series 6.Determine the half range sine series for x f ( x ) 8 x 0 x 4 4 x 8
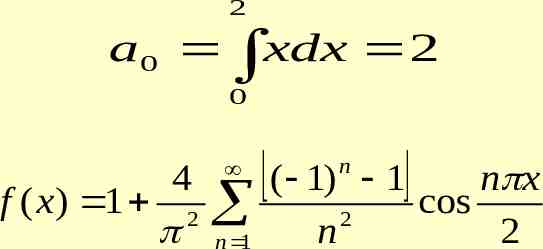
PARSEVAL’S IDENTITY To prove that l 2 1 2 2 2 f ( x ) dx l a ( a b n ) 2 0 n n 1 l Provided the Fourier series for f(x) converges uniformly in (-l, I). The Fourier Series for f(x) in (-l,l) is a0 n x n x f ( x) an cos bn sin .(1) 2 l l n 1 n 1 Multiplying both sides of (1) by f(x)and integrating term from – l to l ( which is justified because f(x) is uniformly convergent)

l a0 n x n x 2 l f ( x) dx 2 n 1 an n 1 f ( x) cos l dx n 1 bn n 1 f ( x) sin l dx a0 la0 an (lan ) bn (lbn ) 2 n 1 n 1 2 a 2 2 2 0 f ( x) dx l (an bn ) .(2) l 2 n 1 l

CASE-I If f(x) is defined in (0,2l) then Parseval’s Identity is given by 2l 2 1 2 2 2 f ( x) dx l a0 (an bn ) .(3) n 1 2 0
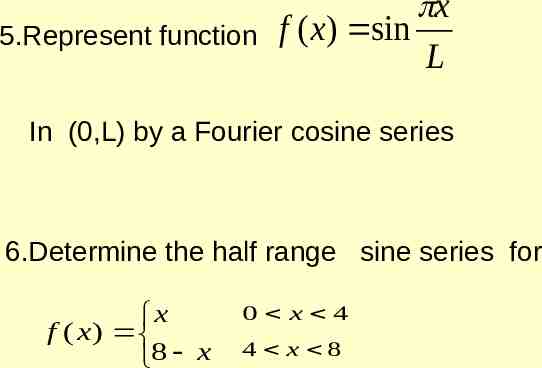
CASE-II If half range cosine series in (o,l) for f(x) is a0 n x f ( x) an cos 2 l n 1 . Then Parseval’s Identity is given by l 2 l 1 2 2 f ( x) dx a0 an .(4) 2 2 n 1 . 0

CASE-III If the half range Sine sereies in (0,l) for f(x) is n x f ( x ) bn sin l n 1 Then Parseval,s Identity is given by l 2 l 2 f ( x ) dx b . .( 5 ) n 2 n 1 0
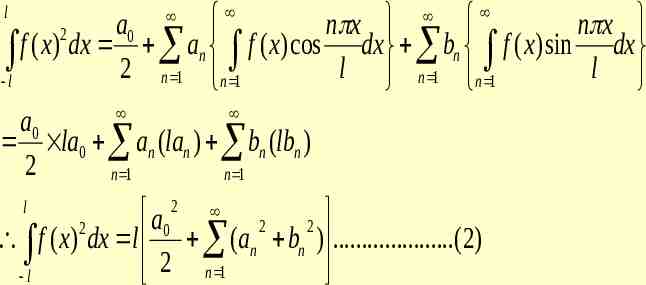
RMS VALUE OF FUNCTION If a function y f(x) is defined in ( c , c 2l ),then 1 2l c 2l 2 y dx c is called the root mean square value (RMS value) of y in ( c , c 2l ).It is denoted by y 1 y 2l 2 c 2l 2 f ( x ) dx c .

Equation(2) becomes 1 2 2 2 y 2l l a0 (an bn ) . 2 n 1 2 y 2 1 2 1 2 2 a0 (an bn ) . 2 n 1 4
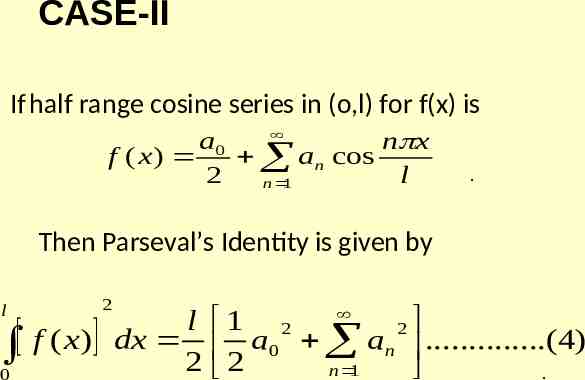
Equation(3) becomes 1 2 2 2 y 2l l a0 (an bn ) . 2 n 1 2 y 2 1 2 1 2 2 a0 (an bn ) . 2 n 1 4
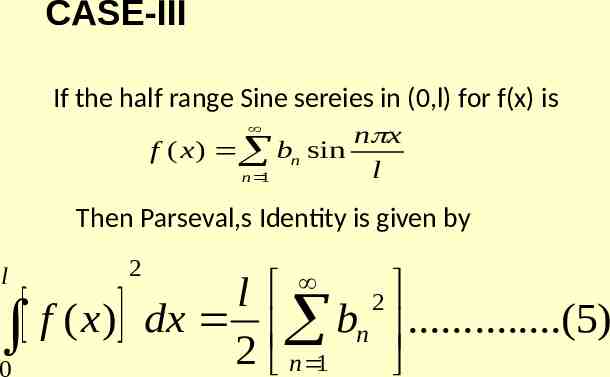
Equation(4) becomes l 1 2 2 a0 a n . 2 2 n 1 2 y l y 2 Equation(5)becomes y 2 1 2 1 2 a0 a n . 2 n 1 4 1 2 bn . 2 n 1

SOLVED PROBLEMS 1) Find the Fourier series of periodic function 2 f ( x) x x in ( , ) Hence deduce the sum of series 1 1 1 1 4 4 4 . 4 1 2 3 4 1 2 2 6 n 1 n Assuming that
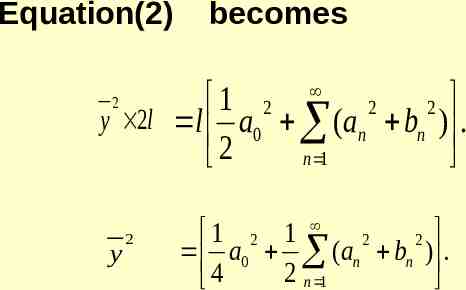
SOLUTION a0 n x n x f ( x) an cos bn sin . 2 n 1 l l n 1 ( , ) in 1 1 2 2 a0 f ( x)dx x dx 3 2
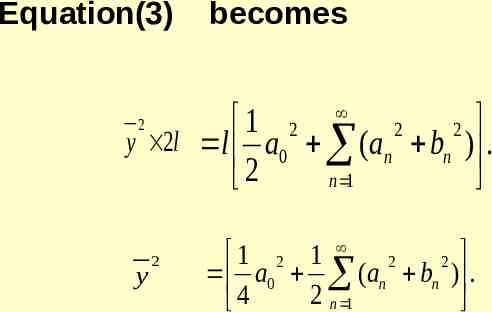
1 an 1 f ( x ) cos nxdx 4 n ( 1 ) n2 bn 1 if 1 2 sin nx cos nx 2 ( x x ) cos nxdx x ( ) 2 x 2 n n n 0 x cos nx is odd function f ( x) sin nxdx 1 2 ( x x) sin nxdx 0 1 x sin nxdx 1 cos nx sin nx 2 n x ( ) 1 ( ) ( 1 ) n n2 n 2 x sin nx is odd function

2 n n ( 1) ( 1) f ( x) 4 2 cos nx 2 sin nx. 3 n n 1 n n 1 in ( , ) Using the Parseval’s Identity 1 1 2 2 2 2 a0 (an bn ) . y 2 n 1 4 y 2 1 2 2 (x 2 x ) dx 4 5 2 3

2 2 4 2 n n a0 ; an 2 ( 1) ; bn ( 1) 3 n n 4 2 4 1 4 1 16 1 4 4 2 5 3 4 9 2 n 1 n 2 n 1 n n 1 1 4 4 n 90 n 1 1 2 2 n 6
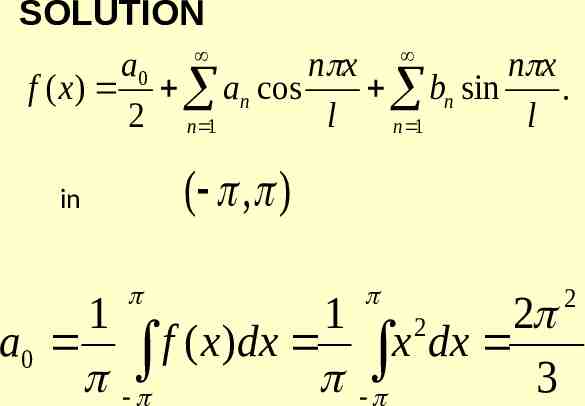
i 2)By using sine series for Show that f ( x) 1 in 0 x 2 1 1 1 1 2 2 2 . 8 3 5 7 SOLUTION n x f ( x) bn sin f ( x ) f ( x ) sin nx l n 1 n 1 bn 2 f ( x) sin nxdx 0 2 1 ( 1) n n for 2 2 cos nx sin nxdx ) ( 0 n 0 n 0
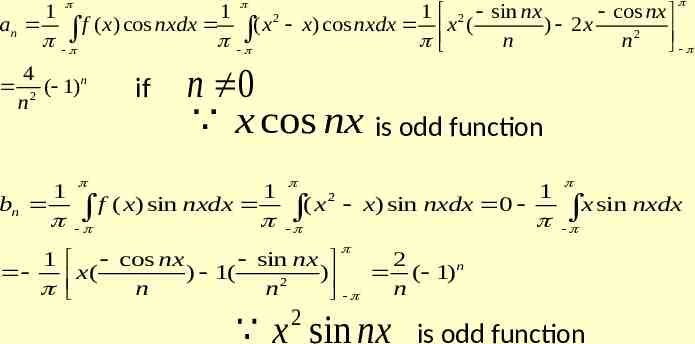
2 n 1 ( 1) f ( x ) 1 sin nx n 1 n By Parseval’s Identity 1 2 bn . 2 n 1 y 1 2 1 4 2 y 1 dx 1 2 2 1 ( 1) n 0 2 n 1 n 2 2 1 1 1 1 2 2 2 . 8 3 5 7 2

0 x l 3)Prove that in l 4l x 1 3 x 1 5 x x 2 (cos 2 cos 2 cos .) 2 n l 3 l 5 l 1 1 1 1 4 and deduce that 14 34 54 7 4 . 96 SOLUTION In Half range cosine series l l 2 2 a0 f ( x ) dx xdx l l 0 l 0
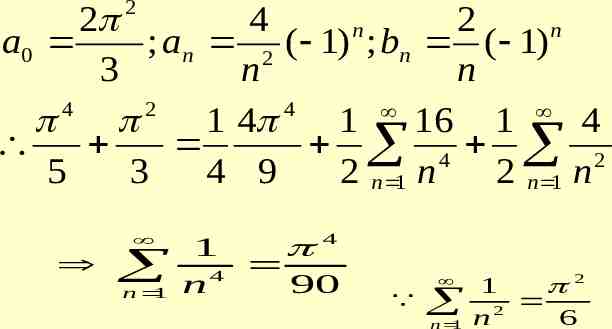
l l 2 n x 2 n x an f ( x) cos dx x cos dx l 0 l l 0 l l n x n x sin cos 2 2l n l l x( ) 1.( ) ( 1 ) 1 2 2 2 2 n n l n 0 l l2 a0 n x f ( x) an cos 2 l n 1 l 1 x 2 2 n 1, 3, 5. 4 n x cos n2 l
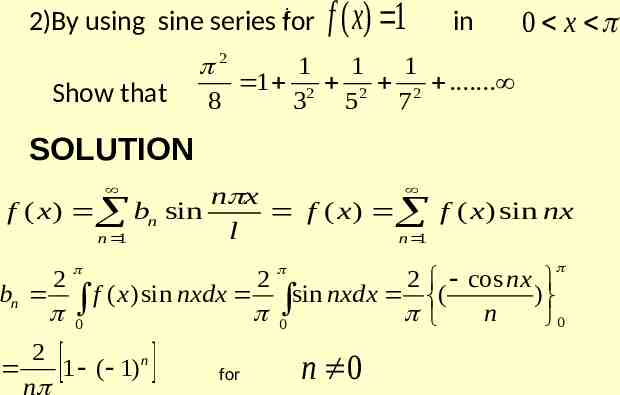
By Parseval’s Identity y 2 1 2 1 2 a0 a n . 2 n 1 4 2 l 1 l 1 l y f ( x ) 2 dx x 2 dx l 0 l 0 3 2 l2 l2 1 4l 2 n 4 4 ( 1) 1 3 4 2 n 1 n 2 1 1 1 1 4 4 4 4 4 . 1 3 5 7 96
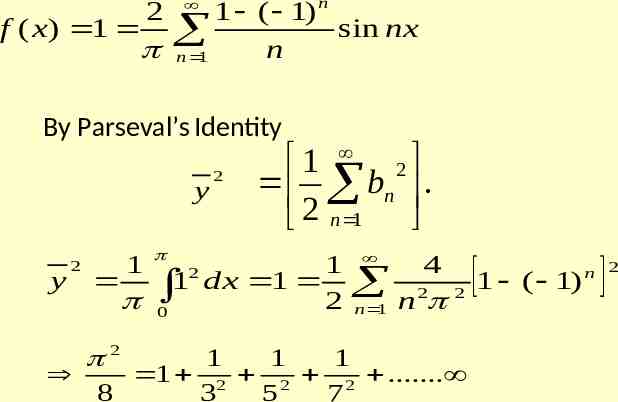
COMPLEX FORM OF FOURIER SERIES The Fourier series of function of period 2l is a periodic a0 n x n x f ( x) an cos bn sin 2 n 1 l l e i e i e i e i cos sin 2 2i n x n x n x n x i i i i a0 e l e l e l e l f ( x ) an bn 2 n 1 2 2i

n x i i n l x f ( x) c0 cn e c n e l n 1 1 1 1 c0 a0 , cn an ibn , c n an ibn 2 2 2 l in x 1 cn f ( x)e l dx for n 0, 1, 2,. 2l l The Fourier series can be represented in the following way
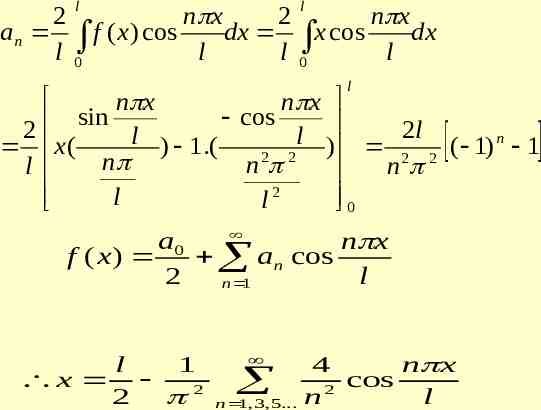
n f ( x ) cn e in x l dx n 1 where cn 2l l f ( x)e in x l dx l SOLVED PROBLEM 1.Find the complex form of the Fourier series of the periodic function 0 when 0 x l f ( x) when l x 2l
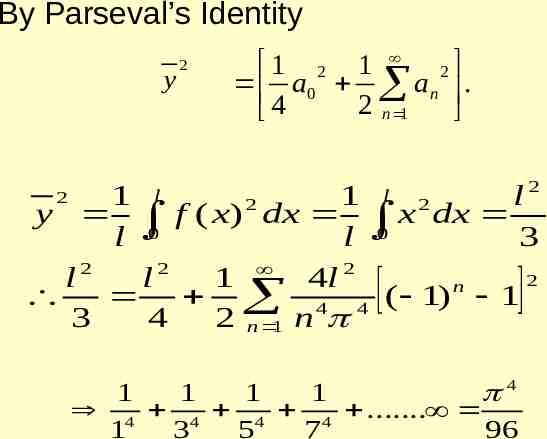
SOLUTION in x f ( x ) cn e l n cn 1 2l 2l f ( x)e in x l dx 0 l in x 1 cn 0 e l 2l 0 l e 2l in 2l in x dx e l dx l in x l 2l l e 2in e ni 2n i

n 1 1 2n i i n 1 1 2 n i in x n f ( x) (1 ( 1) )e l n 2 n 2.Find the complex form of Fourier seriesof f(x) sinx in (0, )

SOLUTION in x f ( x ) cn e 2 n l 2 cn e 2 inx n cn 1 1 2 inx f ( x ) e dx 0 2 inx sin xe dx 0 2 inx 1 e 2in sin x cos x 2 1 4n 0

1 2 in cn e 1 2 4n 1 2 2 4n 1 2 1 2 inx f ( x) e in (0, ) 2 n 4n 1

HARMONIC ANALYSIS a0 f ( x ) an cos nx bn sin nx 2 n 1 a0 1 an bn 1 1 2 f ( x)dx 0 2 f ( x) cos nxdx 0 2 f ( x) sin nxdx 0
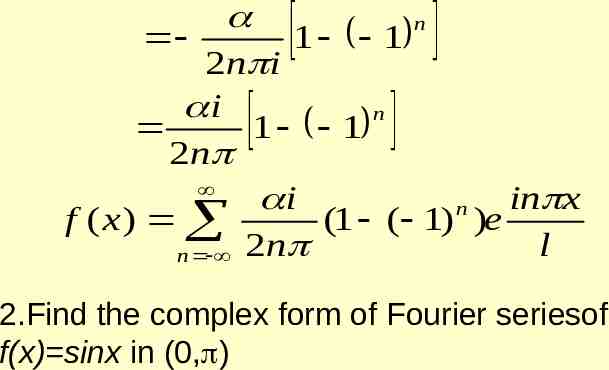
1 a0 2 2 2 f ( x ) dx 2 mean of f ( x ) in 0 , 2 0 1 2 an 2 f ( x ) cos nxdx 2 0 2 mean of f ( x) cos nx in 0,2 2 1 bn 2 f ( x ) sin nxdx 2 0 2 mean of f ( x) sin nx in 0,2
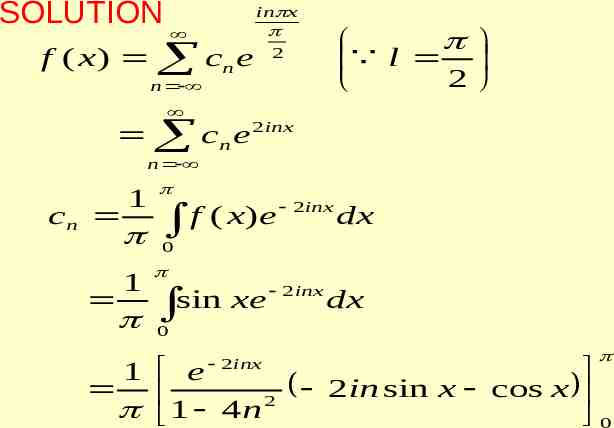
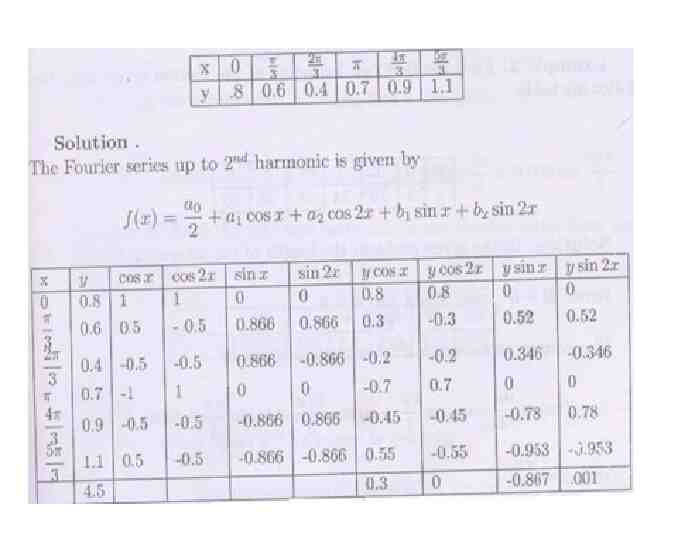
The term a1cosx b1sinx is called the fundamental or first harmonic, the term a2cosx b2sinx is called the second harmonic and so on. Solved Problem 1.Find first two harmonics of Fourier Series from the following table