The Exciting World of Natural Deduction!!! By: Dylan Kane
25 Slides434.50 KB

The Exciting World of Natural Deduction!!! By: Dylan Kane Jordan Bradshaw Virginia Walker

Natural Deduction Gerhard Gentzen Stanislaw Jaskowski 1934 Mimics the natural reasoning process, inference rules natural to humans Called “natural” because does not require conversion to (unreadable) normal form

Background: Natural deduction proofs I’ll be back.

Natural Deduction Proof system for first-order logic Designed to mimic the natural reasoning process Process: Make assumptions (“A” is true) Letters like “A” can represent larger propositional phrases The set of assumptions being relied on at a given step is called the context. Use rules to draw conclusions. Discharge assumptions as they become no longer necessary.

Natural Deduction Natural deduction is done in step by step: Rule Premises Conclusion

Logical Connectives
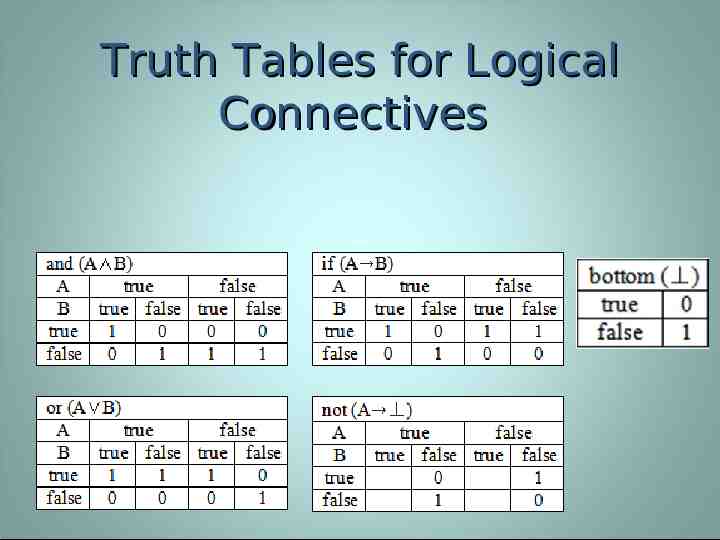
Truth Tables for Logical Connectives

Making Conclusions The rules used to draw conclusions consist mostly of the introduction (I) and elimination (E) of these connectives. Several of the rules serve to discharge earlier assumptions. The result does not rely on the assumption being true. If the assumption is used by itself again somewhere else, it must be discharged again in a step that follows.

Introduction and Elimination Introduction builds the conclusion out of the logical connective and the premises. Elimination eliminates the logical connective from a premise.

Rules: AND/OR Rule “or E” discharges S and T.

Rules: IF Rule “if I” discharges S

Rules: C Proof by contradiction If by assuming S is false, you reach a contradiction, S is true. Discharges (not S)

Rules: forall ( ) Rule “ I” requires that “a” does not occur in S(x) or any premise on which S(a) may depend.

Rules: exists ( ) Rule “ E” requires that “a” does not occur in S(x) or T or any assumption other than S(a) on which the derivation of T from S(a) depends. Rule “ E” also discharges S(a).

Tautology Always true. The proof of a tautology ultimately relies on no assumptions. The assumptions are discharged throughout the proof.

Sample proof: a tautology

Sample proof: a tautology A is discharged using the - I rule.

Sample proof: a tautology B is discharged using the - I rule.

Example using Quantifiers “Imagine how you would convince someone else, who didn’t know any formal logic, of the validity of the entailment you are trying to demonstrate.” a.k.a. That a knowledge base entails a sentence.

Example using Quantifiers Ex. We want to prove this: {forall x (F(x) - G(x)) forall x (G(x) - H(x))} - forall x (F(x) - H(x)) Take an arbitrary object a Suppose a is an F Since all Fs are Gs, a is a G Since all Gs are Hs, a is an H So if a is an F then a is an H But this argument works for any a So all Fs are Hs

Proof using Natural Deduction

Rule exists ( ): Revisited Rule “ E” requires that “a” does not occur in S(x) or T or any assumption other than S(a) on which the derivation of T from S(a) depends. Rule “ E” also discharges S(a).

Incorrect Proof (exists E)

Interesting Tidbits for Further Reading Natural Deduction book written in 1965 by Prawitz Gallier in 1986 used Gentzen’s approach to expound the theoretical underpinning so f automated deduction.

Credits Reeves, Steve and Mike Clarke. Logic for Computer Science. 2003. Russell, Stuart and Peter Norvig. Artificial Intelligence: A modern Approach. 2nd edition. 2003






