Kalman Filtering Jur van den Berg
16 Slides273.10 KB

Kalman Filtering Jur van den Berg

Kalman Filtering (Optimal) estimation of the (hidden) state of a linear dynamic process of which we obtain noisy (partial) measurements Example: radar tracking of an airplane. What is the state of an airplane given noisy radar measurements of the airplane’s position?
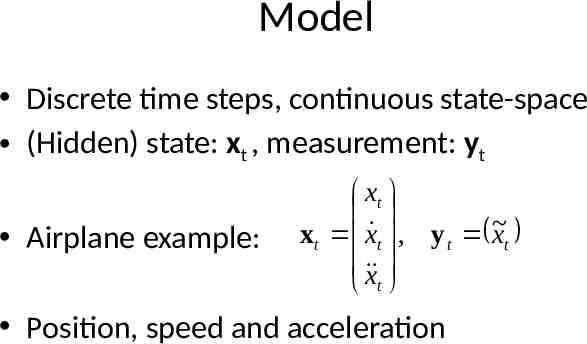
Model Discrete time steps, continuous state-space (Hidden) state: xt , measurement: yt Airplane example: xt x t x t , y t xt x t Position, speed and acceleration

Dynamics and Observation model Linear dynamics model describes relation between the state and the next state, and the observation: x t 1 yt Ax t w t , w t Wt N (0, Q) Cx t v t , v t Vt N (0, R ) Airplane example (if process has time-step ): 1 12 2 A 0 1 , C 1 0 0 0 0 1

Normal distributions Let X0 be a normal distribution of the initial state x0 Then, every Xt is a normal distribution of hidden state xt. Recursive definition: X t 1 AX t Wt And every Yt is a normal distribution of observation yt. Definition: Yt CX t Vt Goal of filtering: compute conditional X t Y0 y 0 , , Yt y t distribution

Normal distribution Because Xt’s and Yt’s are normal distributions, X t Y0 y 0 , , Yt y t is also a normal distribution Normal distribution is fully specified by mean and covariance We denote: X t s X t Y0 y 0 , , Ys y s N E X t Y0 y 0 , , Ys y s , Var X t Y0 y 0 , , Ys y s N xˆ t s , Pt s Problem reduces to computing xt t and Pt t

Recursive update of state Kalman filtering algorithm: repeat – Time update: from Xt t, compute a priori distrubution Xt 1 t – Measurement update: from Xt 1 t (and given yt 1), compute a posteriori distribution Xt 1 t 1 X0 X1 X2 X3 X4 X5 Y1 Y2 Y3 Y4 Y5

Time update From Xt t, compute a priori distribution Xt 1 t: X t 1 t AX t t Wt N E AX t t Wt , Var AX t t Wt N A E X t t E Wt , A Var X t t AT Var Wt N Axˆ t t , APt t AT Q xˆ t 1 t Axˆ t t So, Pt 1 t APt t AT Q

Measurement update From Xt 1 t (and given yt 1), compute Xt 1 t 1. 1. Compute a priori distribution of the observation Yt 1 t from Xt 1 t: Yt 1 t CX t 1 t Vt 1 N E CX t 1 t Vt 1 , Var CX t 1 t Vt 1 N C E X t 1 t E Vt 1 , C Var X t 1 t C T Var Vt 1 N Cxˆ t 1 t , CPt 1 t C T R

Measurement update (cont’d) 2. Look at joint distribution of Xt 1 t and Yt 1 t: X t 1 t E X t 1 t Var X t 1 t Cov X t 1 t , Yt 1 t , N E Yt 1 t Cov Yt 1 t , X t 1 t Var Y t 1 t xˆ t 1 t Pt 1 t Pt 1 t C T , N Cxˆ t 1 t CPt 1 t CPt 1 t C T R , Yt 1 t where Cov Yt 1 , X t 1 t Cov CX t 1 t Vt 1 , X t 1 t C Cov X t 1 t , X t 1 t Cov Vt 1 , X t 1 t C Var X t 1 t CPt 1 t

Measurement update (cont’d) Recall from undergrad that if 1 11 12 Z1 , Z 2 N , 2 21 22 then Z1 Z 2 z 2 N 1 12 221 z 2 2 , 11 12 221 21 Xt 1 t 1 X(Xt 1 t Yt 1 t yt 1): 3. X t Compute Y y 1 t 1 t 1 t t 1 t t 1 T T y Cxˆ , R CP N xˆ t 1 t Pt 1 t C CPt 1 t C R Pt 1 t Pt 1 t C T CPt 1 t C T 1 t 1 t 1 t 1 t 1 t

Measurement update (cont’d): Often written in terms of Kalman gain matrix: K t 1 xˆ t 1 t 1 Pt 1 t 1 T T 1 Pt 1 t C CPt 1 t C R xˆ t 1 t K t 1 y t 1 Cxˆ t 1 t Pt 1 t K t 1CPt 1 t

Kalman filter summary Model: x t 1 Ax t w t , w t Wt N (0, Q) yt Cx t v t , v t Vt N (0, R ) Algorithm: repeat – Time update: xˆ t 1 t Axˆ t t Pt 1 t APt t AT Q – Measurement update: 1 T T K t 1 Pt 1 t C CPt 1 t C R xˆ t 1 t 1 xˆ t 1 t K t 1 y t 1 Cxˆ t 1 t Pt 1 t 1 Pt 1 t K t 1CPt 1 t

Initialization Choose distribution of initial state by picking x0 and P0 Start with measurement update given measurement y0 Choice for Q and R (identity) – small Q: dynamics “trusted” more – small R: measurements “trusted” more

Conclusion Kalman filter can be used in real time Use xt t’s as optimal estimate of state at time t, and use Pt t as a measure of uncertainty.

Extensions Dynamic process with known control input Non-linear dynamic process Kalman smoothing: compute optimal estimate of state xt given all data y1, , yT, with T t (not real-time). Automatic parameter (Q and R) fitting using EM-algorithm






