CPS 170: Artificial Intelligence
29 Slides236.50 KB

CPS 170: Artificial Intelligence http://www.cs.duke.edu/courses/spring09/cps170/ Propositional Logic Instructor: Vincent Conitzer

Logic and AI Would like our AI to have knowledge about the world, and logically draw conclusions from it Search algorithms generate successors and evaluate them, but do not “understand” much about the setting Example question: is it possible for a chess player to have 8 pawns and 2 queens? – Search algorithm could search through tons of states to see if this ever happens, but

A story You roommate comes home; he/she is completely wet You know the following things: – Your roommate is wet – If your roommate is wet, it is because of rain, sprinklers, or both – If your roommate is wet because of sprinklers, the sprinklers must be on – If your roommate is wet because of rain, your roommate must not be carrying the umbrella – The umbrella is not in the umbrella holder – If the umbrella is not in the umbrella holder, either you must be carrying the umbrella, or your roommate must be carrying the umbrella – You are not carrying the umbrella Can you conclude that the sprinklers are on? Can AI conclude that the sprinklers are on?

Knowledge base for the story RoommateWet RoommateWet (RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers) RoommateWetBecauseOfSprinklers SprinklersOn RoommateWetBecauseOfRain NOT(RoommateCarryingUmbrella) UmbrellaGone UmbrellaGone (YouCarryingUmbrella OR RoommateCarryingUmbrella) NOT(YouCarryingUmbrella)

Syntax What do well-formed sentences in the knowledge base look like? A BNF grammar: Symbol P, Q, R, , RoommateWet, Sentence True False Symbol NOT(Sentence) (Sentence AND Sentence) (Sentence OR Sentence) (Sentence Sentence) We will drop parentheses sometimes, but formally they really should always be there

Semantics A model specifies which of the proposition symbols are true and which are false Given a model, I should be able to tell you whether a sentence is true or false Truth table defines semantics of operators: a b NOT(a) a AND b a OR b a b false false true false false true false true true false true true true false false false true false true true false true true true Given a model, can compute truth of sentence recursively with these

Caveats TwoIsAnEvenNumber OR ThreeIsAnOddNumber is true (not exclusive OR) TwoIsAnOddNumber ThreeIsAnEvenNumber is true (if the left side is false it’s always true) All of this is assuming those symbols are assigned their natural values

Tautologies A sentence is a tautology if it is true for any setting of its propositional symbols P Q P OR Q NOT(P) AND (P OR Q) OR NOT(Q) (NOT(P) AND NOT(Q)) false false false true true false true true false true true false true false true true true true false true (P OR Q) OR (NOT(P) AND NOT(Q)) is a tautology

Is this a tautology? (P Q) OR (Q P)
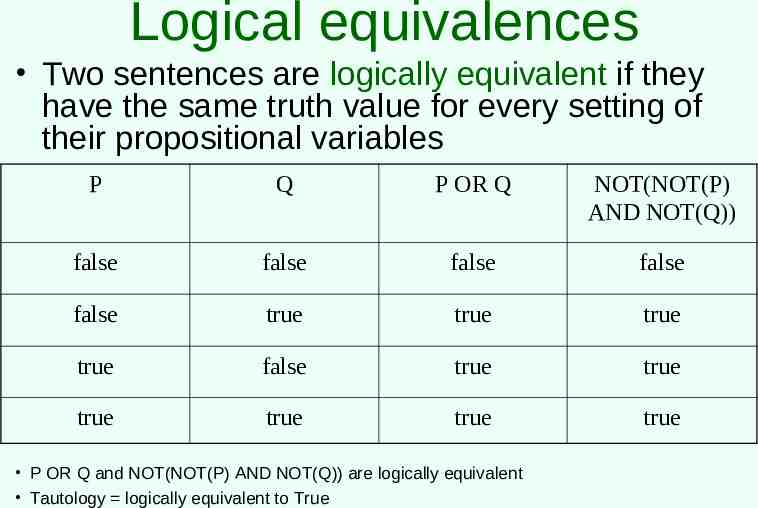
Logical equivalences Two sentences are logically equivalent if they have the same truth value for every setting of their propositional variables P Q P OR Q NOT(NOT(P) AND NOT(Q)) false false false false false true true true true false true true true true true true P OR Q and NOT(NOT(P) AND NOT(Q)) are logically equivalent Tautology logically equivalent to True

Famous logical equivalences (a OR b) (b OR a) commutatitvity (a AND b) (b AND a) commutatitvity ((a AND b) AND c) (a AND (b AND c)) associativity ((a OR b) OR c) (a OR (b OR c)) associativity NOT(NOT(a)) a double-negation elimination (a b) (NOT(b) NOT(a)) contraposition (a b) (NOT(a) OR b) implication elimination NOT(a AND b) (NOT(a) OR NOT(b)) De Morgan NOT(a OR b) (NOT(a) AND NOT(b)) De Morgan (a AND (b OR c)) ((a AND b) OR (a AND c)) distributitivity (a OR (b AND c)) ((a OR b) AND (a OR c)) distributitivity
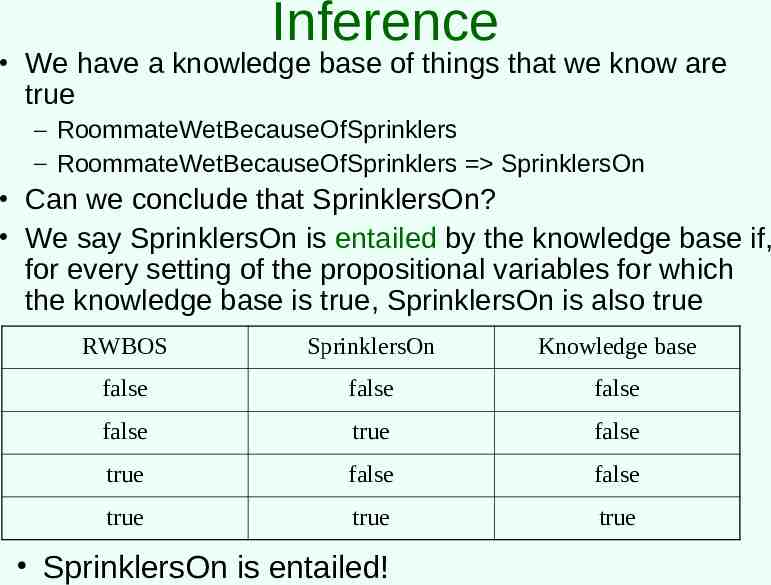
Inference We have a knowledge base of things that we know are true – RoommateWetBecauseOfSprinklers – RoommateWetBecauseOfSprinklers SprinklersOn Can we conclude that SprinklersOn? We say SprinklersOn is entailed by the knowledge base if, for every setting of the propositional variables for which the knowledge base is true, SprinklersOn is also true RWBOS SprinklersOn Knowledge base false false false false true false true false false true true true SprinklersOn is entailed!

Simple algorithm for inference Want to find out if sentence a is entailed by knowledge base For every possible setting of the propositional variables, – If knowledge base is true and a is false, return false Return true Not very efficient: 2#propositional variables settings

Inconsistent knowledge bases Suppose we were careless in how we specified our knowledge base: PetOfRoommateIsABird PetOfRoommateCanFly PetOfRoommateIsAPenguin PetOfRoommateIsABird PetOfRoommateIsAPenguin NOT(PetOfRoommateCanFly) PetOfRoommateIsAPenguin No setting of the propositional variables makes all of these true Therefore, technically, this knowledge base implies anything TheMoonIsMadeOfCheese

Reasoning patterns Obtain new sentences directly from some other sentences in knowledge base according to reasoning patterns If we have sentences a and a b , we can correctly conclude the new sentence b – This is called modus ponens If we have a AND b , we can correctly conclude a All of the logical equivalences from before also give reasoning patterns

Formal proof that the sprinklers are on 1) RoommateWet 2) RoommateWet (RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers) 3) RoommateWetBecauseOfSprinklers SprinklersOn 4) RoommateWetBecauseOfRain NOT(RoommateCarryingUmbrella) 5) UmbrellaGone 6) UmbrellaGone (YouCarryingUmbrella OR RoommateCarryingUmbrella) 7) NOT(YouCarryingUmbrella) 8) YouCarryingUmbrella OR RoommateCarryingUmbrella (modus ponens on 5 and 6) 9) NOT(YouCarryingUmbrella) RoommateCarryingUmbrella (equivalent to 8) 10) RoommateCarryingUmbrella (modus ponens on 7 and 9) 11) NOT(NOT(RoommateCarryingUmbrella) (equivalent to 10) 12) NOT(NOT(RoommateCarryingUmbrella)) NOT(RoommateWetBecauseOfRain) (equivalent to 4 by contraposition) 13) NOT(RoommateWetBecauseOfRain) (modus ponens on 11 and 12) 14) RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers (modus ponens on 1 and 2) 15) NOT(RoommateWetBecauseOfRain) RoommateWetBecauseOfSprinklers (equivalent to 14) 16) RoommateWetBecauseOfSprinklers (modus ponens on 13 and 15) 17) SprinklersOn (modus ponens on 16 and 3)

Reasoning about penguins 1) PetOfRoommateIsABird PetOfRoommateCanFly 2) PetOfRoommateIsAPenguin PetOfRoommateIsABird 3) PetOfRoommateIsAPenguin NOT(PetOfRoommateCanFly) 4) PetOfRoommateIsAPenguin 5) PetOfRoommateIsABird (modus ponens on 4 and 2) 6) PetOfRoommateCanFly (modus ponens on 5 and 1) 7) NOT(PetOfRoommateCanFly) (modus ponens on 4 and 3) 8) NOT(PetOfRoommateCanFly) FALSE (equivalent to 6) 9) FALSE (modus ponens on 7 and 8) 10) FALSE TheMoonIsMadeOfCheese (tautology) 11) TheMoonIsMadeOfCheese (modus ponens on 9 and 10)

Getting more systematic Any knowledge base can be written as a single formula in conjunctive normal form (CNF) – CNF formula: ( OR OR ) AND ( OR ) AND – can be a symbol x, or NOT(x) (these are called literals) – Multiple facts in knowledge base are effectively ANDed together RoommateWet (RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers) becomes (NOT(RoommateWet) OR RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers)

Converting story problem to conjunctive normal form RoommateWet – RoommateWet RoommateWet (RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers) – NOT(RoommateWet) OR RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers RoommateWetBecauseOfSprinklers SprinklersOn – NOT(RoommateWetBecauseOfSprinklers) OR SprinklersOn RoommateWetBecauseOfRain NOT(RoommateCarryingUmbrella) – NOT(RoommateWetBecauseOfRain) OR NOT(RoommateCarryingUmbrella) UmbrellaGone – UmbrellaGone UmbrellaGone (YouCarryingUmbrella OR RoommateCarryingUmbrella) – NOT(UmbrellaGone) OR YouCarryingUmbrella OR RoommateCarryingUmbrella NOT(YouCarryingUmbrella) – NOT(YouCarryingUmbrella)

Unit resolution Unit resolution: if we have l1 OR l2 OR OR lk and NOT(li) we can conclude l1 OR l2 OR li-1 OR li 1 OR OR lk Basically modus ponens

Applying resolution to story problem 1) RoommateWet 2) NOT(RoommateWet) OR RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers 3) NOT(RoommateWetBecauseOfSprinklers) OR SprinklersOn 4) NOT(RoommateWetBecauseOfRain) OR NOT(RoommateCarryingUmbrella) 5) UmbrellaGone 6) NOT(UmbrellaGone) OR YouCarryingUmbrella OR RoommateCarryingUmbrella 7) NOT(YouCarryingUmbrella) 8) NOT(UmbrellaGone) OR RoommateCarryingUmbrella (6,7) 9) RoommateCarryingUmbrella (5,8) 10) NOT(RoommateWetBecauseOfRain) (4,9) 11) NOT(RoommateWet) OR RoommateWetBecauseOfSprinklers (2,10) 12) RoommateWetBecauseOfSprinklers (1,11) 13) SprinklersOn (3,12)

Limitations of unit resolution P OR Q NOT(P) OR Q Can we conclude Q?

(General) resolution General resolution: if we have l1 OR l2 OR OR lk and m1 OR m2 OR OR mn where for some i,j, li NOT(mj) we can conclude l1 OR l2 OR li-1 OR li 1 OR OR lk OR m1 OR m2 OR OR mj-1 OR mj 1 OR OR mn Same literal may appear multiple times; remove those

Applying resolution to story problem (more clumsily) 1) RoommateWet 2) NOT(RoommateWet) OR RoommateWetBecauseOfRain OR RoommateWetBecauseOfSprinklers 3) NOT(RoommateWetBecauseOfSprinklers) OR SprinklersOn 4) NOT(RoommateWetBecauseOfRain) OR NOT(RoommateCarryingUmbrella) 5) UmbrellaGone 6) NOT(UmbrellaGone) OR YouCarryingUmbrella OR RoommateCarryingUmbrella 7) NOT(YouCarryingUmbrella) 8) NOT(RoommateWet) OR RoommateWetBecauseOfRain OR SprinklersOn (2,3) 9) NOT(RoommateCarryingUmbrella) OR NOT(RoommateWet) OR SprinklersOn (4,8) 10) NOT(UmbrellaGone) OR YouCarryingUmbrella OR NOT(RoommateWet) OR SprinklersOn (6,9) 11) YouCarryingUmbrella OR NOT(RoommateWet) OR SprinklersOn (5,10) 12) NOT(RoommateWet) OR SprinklersOn (7,11) 13) SprinklersOn (1,12)

Systematic inference? General strategy: if we want to see if sentence a is entailed, add NOT(a) to the knowledge base and see if it becomes inconsistent (we can derive a contradiction) CNF formula for modified knowledge base is satisfiable if and only if sentence a is not entailed – Satisfiable there exists a model that makes the modified knowledge base true modified knowledge base is consistent

Resolution algorithm Given formula in conjunctive normal form, repeat: Find two clauses with complementary literals, Apply resolution, Add resulting clause (if not already there) If the empty clause results, formula is not satisfiable – Must have been obtained from P and NOT(P) Otherwise, if we get stuck (and we will eventually), the formula is guaranteed to be satisfiable (proof in a couple of slides)

Example Our knowledge base: – 1) RoommateWetBecauseOfSprinklers – 2) NOT(RoommateWetBecauseOfSprinklers) OR SprinklersOn Can we infer SprinklersOn? We add: – 3) NOT(SprinklersOn) From 2) and 3), get – 4) NOT(RoommateWetBecauseOfSprinklers) From 4) and 1), get empty clause

If we get stuck, why is the formula satisfiable? Consider the final set of clauses C Construct satisfying assignment as follows: Assign truth values to variables in order x1, x2, , xn If xj is the last chance to satisfy a clause (i.e., all the other variables in the clause came earlier and were set the wrong way), then set xj to satisfy it – Otherwise, doesn’t matter how it’s set Suppose this fails (for the first time) at some point, i.e., xj must be set to true for one last-chance clause and false for another These two clauses would have resolved to something involving only up to xj-1 (not to the empty clause, of course), which must be satisfied But then one of the two clauses must also be satisfied contradiction

Special case: Horn clauses Horn clauses are implications with only positive literals x1 AND x2 AND x4 x3 AND x6 TRUE x1 Try to figure out whether some xj is entailed Simply follow the implications (modus ponens) as far as you can, see if you can reach xj xj is entailed if and only if it can be reached (can set everything that is not reached to false) Can implement this more efficiently by maintaining, for each implication, a count of how many of the left-hand side variables have been reached






